|
||||
|
Раздел 2. ОРГАНИЗАЦИЯ ТЯГОТЕНИЯ В «ЦИФРОВОМ» МИРЕ 2.1. Вы полагаете, что тяготение порождается массами? Закон всемирного тяготения, как его сформулировал Ньютон, имел чисто постулативный характер. На основе наблюдений за движением небесных тел и за падением малых тел на Землю декларировалось, что любые две массочки во Вселенной притягиваются друг к другу с силой, равной
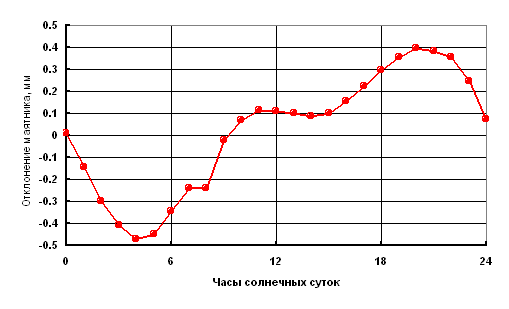
где G - гравитационная постоянная, m1 и m2 - притягивающие друг друга массочки, R - расстояние между ними. Мало кто знает: из ускорений свободного падения к большим космическим телам – к Солнцу и планетам – определяются лишь произведения гравитационной постоянной G на массы этих тел, но сами эти массы отнюдь не определяются. Если принятое значение G было бы, скажем, в два раза больше, а принятые массы Солнца и планет были бы в два раза меньше (или наоборот) – то это никак не отразилось бы на результатах теоретического анализа движения тел в Солнечной системе. Т.е., принятые значения масс Солнца и планет продиктованы принятым значением гравитационной постоянной. А совпадают ли эти принятые значения масс с их истинными значениями, соответствующими количеству вещества в Солнце и планетах – науке это неизвестно до сих пор. С чего же Ньютон влепил в формулу (2.1.1) произведение масс? – это на его совести. Но стало так: больше масса – сильнее притяжение к ней, меньше масса – слабее притяжение к ней, совсем нет массы – совсем нет притяжения к ней… Значит, чем порождается это притяжение? Конечно, массой – это же чисто математически ясно! Но физически-то это было совсем не ясно. Чем обусловлено взаимное притяжение массивных тел – Ньютон не пояснил. Всё, что он сказал по этому поводу – это что массивные тела действуют друг на друга на расстоянии через некоторого посредника. Но пускаться в рассуждения о природе этого посредника означало бы прибегать к гипотезам – а гипотез, как полагал Ньютон, он «не измышлял». С тех пор людям вдалбливали, что каждое массивное тело обладает таким хорошо известным свойством: притягивать остальные массивные тела. Если находился кто-то, в этом сомневавшийся, то его сбрасывали с высоты – достаточной, чтобы ушибиться насмерть – после чего спрашивали: «Ну, теперь понял, что Земля тебя притягивает?» Это действовало безотказно – последние сомнения отпадали. И вот, в таком режиме прошло триста лет. Сменилось множество поколений. Сейчас даже детишки, шлёпнувшись и потирая набитую шишку, приговаривают: «Это всё из-за притяженья Земли!» Вундеркинды, однако. Им, конечно, невдомёк, что за триста лет наука ничуть не продвинулась в понимании физики того, как это «притяженье Земли» действует – каким образом масса притягивает другую массу на расстоянии. Тут академики переглянутся и с умным выраженьем на лице заявят, что всё они тут прекрасно понимают: согласно Эйнштейну, мол, каждая массочка искривляет вокруг себя пространство-время, и это искривление действует на остальные массочки… Вот! Легко убедиться, что здесь-то у академиков «прекрасное понимание» и заканчивается. Задайте им простейшие и сразу напрашивающиеся вопросы: что такое, физически, искривление пространства-времени? как, физически, масса его порождает? и как оно, физически, действует на другие массы? Уверяем: простых и чётких ответов, свидетельствующих о знании предмета, вы не получите. Будет прямо как в случае со студентом, нашим одногруппником, который довёл экзаменаторшу до того, что она воскликнула: «Ну что Вы, как собака – всё понимаете, но ничего сказать не можете!» А ведь это симптоматично – что за триста лет наука ни на йоту не продвинулась в понимании физики тяготения. Что-то тут не так. Чем же занимались толпы учёных мужей эти триста лет – груши околачивали, что ли? Нет, у них были занятия поважнее. Они проделали титаническую работу по извращению экспериментальных реалий, чтобы скрыть факты, которые с очевидностью свидетельствуют о том, что тяготение порождается НЕ массами, что массы лишь подчиняются тяготению, но сами они не притягивают. Мы расскажем об этих фактах. Их – не один, не два. Их много. Причём, мы расскажем лишь о тех, до которых нам удалось докопаться. Едва ли можно сомневаться в том, что наш перечень подобных фактов [Г16] – далеко не исчерпывающий, и что полная картина высоконаучной лжи на тему тяготения – гораздо грандиознее. 2.2. Как Кавендиш и его последователи получали «притяжение» между лабораторными болванками. Считается, что первый эксперимент, который доказал наличие гравитационного притяжения между лабораторными болванками – это знаменитый опыт Кавендиша (1798 г.). Казалось бы, ввиду исключительной важности этого опыта, его технические и методические подробности должны быть легко доступны. Учитесь, мол, студенты – как ставить фундаментальные эксперименты! Но не тут-то было. Студентам скармливают до неприличия адаптированную версию. Дескать, Кавендиш использовал крутильные весы: это горизонтальное коромысло с грузиками на концах, подвешенное за свой центр на тонкой упругой струне. Оно может поворачиваться в горизонтальной плоскости, закручивая упругий подвес. Кавендиш, якобы приблизил к грузикам коромысла пару болванок – с противоположных сторон – и коромысло повернулось на небольшой угол, при котором момент сил гравитационного притяжения грузиков к болванкам уравновесился упругой реакцией подвеса на закручивание. Вот и всё, ребята! Усвоили? Молодцы! Всем – по пять баллов! А подробностями вы не заморачивайтесь! Но ведь это странно, чёрт возьми! Даже в специализированных изданиях, вроде [С1], подробности опыта Кавендиша не излагаются! Счастье, что нам удалось до них добраться в книге по истории физики [Г1], где дан перевод первоисточника – труда самого Кавендиша. Это – дивный сон какой-то. Методика, которую использовал Кавендиш, наглядно показывает, что гравитационным притяжением болванок там и не пахло! Смотрите: крутильные весы Кавендиша – это высокочувствительная система, которая совершает долгопериодические и высокодобротные свободные колебания. Их трудно успокоить. Поэтому идея опыта заключалась в следующем: после перемещения болванок из дальней «непритягивающей» позиции в ближнюю «притягивающую», коромысло должно было продолжить свои колебания – довернувшись так, чтобы средние положения грузиков приблизились к болванкам. И как же эта идея реализовалась? Да уж пришлось попыхтеть! Исходное положение: коромысло колеблется, а болванки находятся в дальней, «непритягивающей» позиции. Если ожидается, что, в результате их перемещения в ближнюю позицию, коромысло довернётся к новому среднему положению колебаний, то когда следует перемещать болванки, чтобы этот доворот коромысла проявился в наиболее чистом виде? Конечно же, когда коромысло проходит нынешнее среднее положение и движется в сторону ожидаемого доворота. Именно так и делалось. И – о, чудо! – коромысло начинало доворот. Казалось бы – дождись, когда выявится новое среднее положение, и дело в шляпе! Ан нет. Вот что писал Кавендиш: «…в этом опыте притяжение грузов отклоняло коромысло с деления 11.5 до деления 25.8 [это средние положения]… после того, как коромысло приближалось к делению 15, я возвращал грузы в среднюю [дальнюю] позицию и оставлял их там до того момента, когда коромысло подходило близко к крайней точке своего колебания, и тогда снова сдвигал грузы в положительную [ближнюю] позицию» [Г1]. Обратите внимание: вскоре после первого перемещения болванок в «притягивающую» позицию и начала движения коромысла к новому среднему положению, болванки возвращали в «непритягивающую» позицию. А затем, в самом конце доворота коромысла, болванки вновь перемещали в «притягивающую» позицию. В итоге этой эффектной трёхходовки болванок оказывалось, что они находятся в ближней, «притягивающей» позиции, а коромысло колеблется, довернувшись к ним – как будто и впрямь из-за гравитационного притяжения. Но «гравитационная» интерпретация здесь никак не проходит, поскольку три четверти пути к новому среднему положению коромысло поворачивалось в то время, когда болванки находились в дальней позиции и, по логике эксперимента, «не притягивали». А ведь смещение к новому среднему положению превышало амплитуду свободных колебаний коромысла в семь раз! Какая же нечистая сила доворачивала коромысло, если это было не притяжение болванок? Есть основания полагать, что «секрет успеха» Кавендиша был связан с микровибрациями, под воздействием которых изменялись параметры крутильных весов, так что весы изменяли своё поведение. Это изменение заключается в следующем. Пусть, при прохождении коромыслом среднего положения, начинаются микровибрации – например, у кронштейна, к которому прикреплён подвес коромысла. Опыт применения вибраций в технике [Б1] показывает, что под действием микровибраций эффективная жёсткость подвеса должна уменьшиться: струна как бы размягчится. И, значит, коромысло отклонится от среднего положения на существенно большую величину, чем при свободном отклонении без микровибраций. Причём, если это увеличенное отклонение не превысит некоторую критическую величину, то будет возможен ещё один интересный эффект. А именно: если микровибрации прекратятся до того, как коромысло достигнет максимального отклонения, то возобновятся свободные колебания с прежней амплитудой, но со смещённым средним положением. Более того, этот эффект будет обратим: новым подходящим добавлением микровибраций можно будет вернуть колебания коромысла к их прежнему среднему положению. Таким образом, поведение крутильных весов у Кавендиша вполне могло быть обусловлено всего лишь подходящими добавлениями микровибраций к крутильным колебаниям коромысла. К тому же, источник микровибраций в данном случае достаточно очевиден. Конструкция установки была бесхитростная: кронштейн с подвешенной к нему чувствительной крутильной системой был прикреплён к боковой стенке того же самого деревянного корпуса, к крышке которого крепился ворот с подвесками двух болванок – по 158 кг каждая. Ясно, что при каждом перемещении болванок неизбежно возникали вибрации, которые передавались на чувствительную крутильную систему. В той самой трёхходовке, вибрации из-за первых двух подвижек болванок обеспечивали требуемый доворот коромысла, а вибрации из-за третьей подвижки пропадали зря, приходясь на замирание коромысла вблизи крайнего отклонения. Всё сходится! Потому и не афишируют подробности опыта Кавендиша: он не обладает никакой доказательной силой. Неоткуда было взяться «отношению сил притяжения грузика к Земле и к болванке с известной массой», поскольку измеряемый эффект был обусловлен вовсе не притяжением грузиков к болванкам. А то, что измеряемый эффект оказался правдоподобен, можно объяснить результатом подгонки. Ведь известно, что перед своими измерениями Кавендиш долго переделывал и настраивал доставшуюся ему установку [Г1]. По-видимому, поначалу на ней неправдоподобные результаты получались. А правдоподобный результат Кавендиш знал заранее, поскольку Ньютон уже дал умозрительную оценку средней плотности Земли: «так как обыкновенные верхние части Земли примерно вдвое плотнее воды, немного ниже, в рудниках, оказываются примерно втрое, вчетверо и даже в пять раз более тяжёлыми, правдоподобно, что всё количество вещества Земли в пять или шесть раз более того, как если бы оно всё состояло из воды» (цитируется по [С1]). Авторитет Ньютона был велик, поэтому, хотя разные исследователи получали очень разные значения, сообщали они, конечно, только о тех, которые оказывались «правдоподобными». Результат долгого применения такого подхода вполне закономерен: оказалось, что Ньютон «с гениальной прозорливостью назвал, практически, современное значение средней плотности Земли» [С1]. Следует лишь уточнить, что это «современное значение» (?5.5 г/см3 [А1]) не является непредвзятым: оно находится в том самом ряду «правдоподобных» значений. А нас ещё уверяют, что результат Кавендиша был впоследствии неоднократно повторён его последователями! Вот интересно: если в первом результате желаемое выдавалось за действительное, то могло ли быть по-другому в его повторениях? Многие из статей последователей Кавендиша труднодоступны, а по их комментариям в специализированных обзорах, например, в [С1], невозможно проследить происхождение итоговых цифр. Недомолвки характерны и для тех статей [Р1,Л1,К1], с которыми нам удалось ознакомиться. А вот показательная статья [С2], авторы которой повторяли опыт Кавендиша на прецизионной установке в ГАИШе – и, якобы, обнаружили притяжение лабораторных болваночек в полном согласии с законом всемирного тяготения. Только загвоздка в том, что это притяжение не обнаруживается напрямую, и для «полного согласия» авторам пришлось прибегнуть к методу оптимизации многих параметров. Этот метод – настоящая находка! Он позволяет высоконаучно доказывать наличие эффектов, которые не существуют в действительности. Это делается так. Записывают навороченные, со множеством параметров, дифференциальные уравнения, в которых – это ключевой момент! – желаемый эффект учитывается так, как будто он существует. Получают экспериментальные данные. А затем, с помощью быстродействующего компьютера, проводят процедуру оптимизации – подгоняя значения параметров для наилучшего согласия теории, где желаемый эффект есть, с практикой, где желаемого эффекта нет. После этого считают, что получено наилучшее согласие теории с опытом – налицо же оптимизация, как ни крути. Во времена Кавендиша о таких мощных методах познания даже не мечтали! Но вот – необычная статья [Г2]. В ней авторы достаточно подробно изложили, что и как они делали. Схематическое изображение их установки мы воспроизводим на Рис.2.2. Использовались не крутильные весы в традиционном варианте, а подвешенная на 17-микронной вольфрамовой нити плоская стеклянная пластинка (1.5?76.0?41.6 мм). Притягивающие массы, четыре стальных шара по 8.14 кг, располагались в одной вертикальной плоскости, проходящей через ось подвеса, как показано на рисунке – причём столик, несущий эти шары, мог прецизионно поворачиваться. Если есть притяжение элементов объёма стеклянной пластинки к стальным шарам, то на пластинку должен действовать крутящий момент, знак и величина которого зависят от угла между плоскостью пластинки и плоскостью центров шаров. За один полный поворот столика с шарами, этот крутящий момент должен испытать два полных колебания. Эти колебания регистрировали так. Столик приводили в медленное вращение с постоянной скоростью, и включали слежение за ориентацией пластинки. Если пластинка начинала поворачиваться, то система обратной связи подавала на двигатель столика такое дополнительное управление, чтобы скорость вращения столика относительно пластинки поддерживалась, по возможности, постоянной. При этом угловое ускорение столика считалось искомым полезным эффектом – и авторы привели его типичную экспериментальную синусоиду. Всё у них было по последнему слову техники: и воздушные подшипники у столика, и протестированные ультразвуком шары, и вакуум, и магнитное экранирование, и контроль температуры – и даже кварцевый генератор в петле обратной связи они прокалибровали с помощью GPS-приёмника. Ну, всё – супер-пупер! Поэтому и выложили всё на всеобщее обозрение. Думали – никто не подкопается. А мы взяли да подкопались. Вот, смотрите. Допустим, что элементы объёма пластинки и вправду притягиваются к шарам. Тогда действующий на пластинку крутящий момент будет обращаться в нуль, когда плоскость пластинки будет либо параллельна к плоскости шаров, либо перпендикулярна к ней. Но максимальные значения крутящего момента будут достигаться не точно посередине между нулями – они будут сдвинуты к нулям, соответствующим параллельным положениям плоскостей пластинки и шаров. Мы не поленились и выполнили соответствующее математическое моделирование для реальной геометрии установки [Г2]. Оказалось, что стягивания-растягивания результирующей синусоиды должны быть заметны даже невооружённым глазом – и уж тем более с использовавшимся энкодером, имевшим разрешение в 100 шагов на градус. Но экспериментальный график в [Г2] представляет собой идеальную синусоиду! Значит, эта идеальная синусоида никак не могла быть результатом гравитационного взаимодействия пластинки с шарами. Что же нам подсунули? Да ещё под это дело «уточнили» значения масс Земли и Солнца!
Рис.2.2 Вот интересно: при том, что попытки профессиональных экспериментаторов обнаружить гравитационное притяжение между лабораторными болваночками представляли собой сплошные проколы, фирма PASCO [П4] наладила выпуск настольных установок «для повторения фундаментального эксперимента Кавендиша». Похоже, руководители этой фирмы полагают, что, приобретя их игрушку, любая домохозяйка утрёт нос всем горе-профессионалам. Ведь в Инструкции по применению [П5] приводится аж три способа измерения гравитационной постоянной! Впрочем, один из них основан на том же трюке, что и у Кавендиша: смена позиций «притягивающих» шаров производится при подходящей фазе колебаний коромысла крутильных весов, отчего происходит сдвиг положения равновесия коромысла – причём, в нужную сторону. Зато ещё два способа работают благодаря вращательным уклонениям местной вертикали – феномену, который официальная наука не признаёт, поскольку он убийственен для закона всемирного тяготения. Мы вернёмся к этому вопросу в 2.15. 2.3. О чём говорит нам форма геоида. Если бы Земля была однородным шаром, то, согласно закону всемирного тяготения, гравитационная сила, действующая на пробное тело вблизи поверхности Земли, зависела бы лишь от расстояния до её центра. Но Земля является сплюснутым эллипсоидом, имея так называемую «экваториальную выпуклость». Экваториальный радиус Земли равен приблизительно 6378.2 км, а полярный – 6356.8 км [А1]. Из-за одного того, что экваториальный радиус Земли больше полярного, гравитационная сила на экваторе должна быть несколько меньше, чем на полюсе. Причём, считается, что форма геоида является гидродинамически равновесной, т.е. что экваториальная выпуклость образовалась не без помощи центробежных сил, обусловленных собственным вращением Земли. Если найти приращение ?R экваториального радиуса из условия, что результирующее уменьшение гравитационного ускорения на экваторе равно центробежному ускорению на экваторе, то для ?R мы получим величину 11 км [Г3]. Заметим, что если земной шар превращается в сплюснутый эллипсоид при сохранении своего объёма, то, в согласии с формулой для объёма эллипсоида, увеличение экваториального радиуса на 11 км вызовет уменьшение полярного радиуса на те же 11 км. Итоговая разность составит 22 км, т.е. величину, близкую к фактической. Значит, модель гидродинамически равновесной формы геоида очень похожа на правду. А теперь обратим внимание на то, что в расчётах мы не учитывали гравитационное действие вещества, находящегося в объёме экваториальной выпуклости – это действие, имей оно место, было бы отнюдь не одинаково при гравиметрических измерениях на экваторе и на полюсе. При гравиметрических измерениях на полюсе, действие всей экваториальной выпуклости было бы на порядок меньше, чем действие небольшой характерной части экваториальной выпуклости, прилегающей к точке проведения измерений на экваторе. Поэтому, из-за наличия экваториальной выпуклости, сила тяжести на экваторе была бы дополнительно увеличена по сравнению с силой тяжести на полюсе – и, значит, равновесное увеличение экваториального радиуса ?R было бы несколько меньше полученного нами значения в 11 км. Наши расчёты [Г3] показывают, что, при средней плотности вещества в объёме экваториальной выпуклости, равной 3000 кг/м3, ?R составило бы 7.8 км – что существенно отличается от фактической величины. Таким образом, если экваториальная выпуклость обладала бы притягивающим действием, то гидродинамически равновесная форма геоида заметно отличалась бы от фактической. Но эти заметные отличия не наблюдаются. Отсюда мы делаем вывод: сотни триллионов тонн вещества экваториальной выпуклости Земли не обладают притягивающим действием. Этот поразительный, «лежащий на поверхности» вывод до сих пор никто не оспорил. Разве что баллистики, которые рассчитывают движение искусственных спутников Земли, уверяли нас, что они учитывают, в своих расчётах, гравитационное действие экваториальной выпуклости. Ну, что тут поделаешь. Мы-то знаем, что при оптимизации многих параметров именно это и делают: учитывают несуществующие эффекты. Всё нормально! 2.4. Оглушительные результаты гравиметрических измерений. Поверхностные массы Земли распределены неоднородно. Там есть мощные горные массивы, с плотностью пород около трёх тонн на кубометр. Есть океаны, в которых плотность воды составляет всего тонну на кубометр – даже на глубине в 11 километров. Есть долины, лежащие ниже уровня моря – в которых плотность вещества равна плотности воздуха. По логике закона всемирного тяготения, эти неоднородности распределения масс должны действовать на гравиметрические инструменты. Простейшим гравиметрическим инструментом является отвес – успокоившись, он ориентирован вдоль местной вертикали. Издавна предпринимались попытки обнаружить уклонения отвеса, обусловленные притяжением, например, мощных горных массивов. Только роль отвеса здесь играл, конечно, не простой грузик на ниточке – ибо как можно знать, куда и насколько он отклонён? А использовался метод сравнения геодезических координат пункта измерений (получаемых, например, с помощью триангуляции) и его же координат, получаемых из астрономических наблюдений. Лишь во втором из этих методов используется привязка к местной вертикали, которая реализуется, например, с помощью ртутного горизонта у телескопа. Таким образом, по разнице координат пункта, полученных названными двумя методами, можно судить об уклонении местной вертикали. Так вот, результирующие уклонения в большинстве случаев оказались гораздо меньше тех, которые ожидались из-за действия горных массивов. Во многих учебниках по гравиметрии (см., например, [Ц1,Ш1]) упоминаются измерения, которые в середине 19-го века провели англичане южнее Гималаев. Там ожидались рекордные уклонения, ведь с севера находился самый мощный горный массив Земли, а с юга – Индийский океан. Но обнаруженные уклонения оказались почти нулевыми. Аналогичное поведение отвеса обнаруживается и вблизи морской береговой линии – вопреки ожиданиям того, что суша, более плотная, чем морская вода, будет притягивать отвес сильнее. Для объяснения подобных чудес учёные приняли гипотезу об изостазии. Согласно этой гипотезе, действие неоднородностей поверхностных масс скомпенсировано действием неоднородностей противоположного знака, находящихся на некоторой глубине. Т.е., под поверхностными плотными породами должны находиться рыхлые, и наоборот. Причём, эти верхние и нижние неоднородности должны, совместными усилиями, повсеместно обнулять действие на отвес – как будто никаких неоднородностей нет вовсе. Знаете, когда читатели наших статей доходили до мест про изостазию, то они, не веря возможности такого лепета в современной науке, кидались, например, в Википедию – и убеждались, что всё так и есть. И – как они выражались – «от хохота падали пацтул». Ну, действительно: чем глубже океан, тем мощнее плотные компенсирующие залежи под его дном. А чем выше горы, тем на всё более рыхлом фундаменте они красуются. Причём, всё – тютелька в тютельку! Даже детям смешно! Но дети ещё не знают, что концепция изостазии прямо противоречит реалиям динамики земной коры [М1] – а то они смеялись бы ещё громче. Заметим, что уклонения отвеса свидетельствуют о горизонтальных компонентах местного вектора силы тяжести. Вертикальная же его компонента определяется с помощью гравиметров. С гравиметрами творятся те же самые чудеса, что и с отвесами. Но измерений с гравиметрами – очень много. Поэтому, чтобы народ не смешить, специалисты нагромоздили терминологические и методологические дебри, сквозь которые трудно продраться непосвящённому. Если публиковать прямые результаты гравиметрических измерений, то было бы слишком очевидно, что они не зависят от поверхностных неоднородностей масс. Поэтому прямые результаты пересчитывают, внося специальные поправки. Первая поправка, «за свободный воздух», или «за высоту», отражает нахождение пункта измерений на высоте, не совпадающей с уровнем моря (вблизи поверхности Земли эта поправка составляет около 0.3 мГал/м; 1 Гал = 1 см/с2). Вторая поправка отражает действие поверхностных неоднородностей масс. Сумму этих поправок называют поправкой Буге. Разность между измеренным и теоретическим значениями силы тяжести называют аномалией: без учёта второй поправки эта разность называется аномалией в свободном воздухе, а с учётом обеих – аномалией Буге. Теперь процитируем [Ш1]: «…пределы изменений аномалий в свободном воздухе должны быть от –350 мГал (для океана глубиной 5 км) до +450 мГал (для плоскогорья высотой 4 км). Аномалии Буге должны равняться нулю. Однако оказалось, что результаты наблюдений противоречат этой теоретической зависимости. Аномалии в свободном воздухе почти не выходят за пределы ±50 мГал, а огромное большинство аномалий вообще близко к нулю. В то же время аномалии Буге в горных районах оказываются, как правило, отрицательными и довольно значительными по величине. Так, в западном Тибете, Памире, Куэнь-Луне аномалии Буге колеблются в пределах от –250 мГал до –550 мГал, в Мексиканском нагорье достигают –200 мГал, в Альпах –150 мГал. Напротив, в Атлантическом и Тихом океанах они имеют положительные значения от 300 до 400 мГал. » «…длинные полосы отрицательных аномалий… прослеживаются вдоль западного берега Южной и Центральной Америки, вдоль Алеутской островной дуги,… вдоль внешнего края дуги Суматра-Ява, вдоль Пуэрто-Рико, по дуге Южных Сандвичевых островов… Всюду эти аномалии или совпадают с глубоководными желобами, или идут по их краю». Таким образом, имеет место чёткая закономерность: если при гравиметрической съёмке не вводить поправок на влияние поверхностных масс, а использовать только поправку «за свободный воздух», то аномалии силы тяжести везде становятся близкими к нулю. Но считается, что поверхностные массы не могут не оказывать влияния на гравиметр, поэтому вычисляются и вносятся поправки, которые и дают аномалии, равные по величине этим поправкам. А затем, чтобы обнулить аномалии и привести теоретические значения в согласие с измеренными, применяют всё ту же остроумную гипотезу об изостазии. Думаете, не может быть такого плачевного состояния дел в науке? Может, может. А вот чего не может быть – так это изостатической компенсации. И по очень простой причине. Вот, пусть под поверхностью грунта находится локальное включение с повышенной плотностью, а под ним – компенсирующее включение с пониженной плотностью. Заметим, что если сила тяжести над этими включениями равна силе тяжести над участком с нормальной плотностью, то в стороне от этих включений компенсация уже не имеет места: изостатический диполь «притягивает» иначе, чем аналогичный участок с нормальной плотностью, что должно вызвать соответствующее уклонение отвеса. При заданном неоднородном распределении поверхностных масс, никаким распределением компенсирующих масс нельзя добиться сразу и нулевых уклонений отвеса, и нулевых аномалий силы тяжести: изостазия для отвесов и изостазия для гравиметров - несовместимы. На практике же повсеместно нулевые уклонения отвеса наблюдаются вместе с нулевыми аномалиями силы тяжести (если не вводить излишних поправок). Т.е. практика с полной очевидностью показывает: гравиметрические инструменты не реагируют на распределение масс. А почему? Наука до сих пор не выработала ответа на этот вопрос. А мы отвечаем: потому что массы не обладают притягивающим действием. И не только для поверхностных масс Земли справедлив этот вывод – гравиметрия позволяет обобщить его на всё вещество Земли. Это возможно с помощью измерений под поверхностью геоида, проводимых в шахтах или на борту погрузившегося под воду батискафа. Смотрите: согласно закону всемирного тяготения, земная сила тяжести в приближении, когда Земля считается однородным невращающимся шаром, максимальна на поверхности этого шара. Ведь, при подъёме над поверхностью, ускорение свободного падения уменьшается согласно выражению GMЗ/r2, где G - гравитационная постоянная, MЗ - масса Земли, r - расстояние до её центра. А, при погружении под поверхность, ускорение свободного падения уменьшается из-за того, что уменьшается «притягивающая» масса, поскольку равно нулю суммарное действие масс в поверхностном шаровом слое с толщиной, равной глубине погружения. При этом ускорение свободного падения линейно зависит от расстояния до центра Земли: GMЗr/R3, где R - радиус Земли. Таким образом, в названном приближении, на поверхности Земли имел бы место излом (а также смена знака!) зависимости ускорения свободного падения от расстояния до центра Земли. Если же, как мы утверждаем, тяготение порождается не массами, и геометрия частотных склонов (1.6) задана независимо от распределения масс, то и у зависимости ускорения свободного падения от высоты нет излома на поверхности Земли – функция ~1/r2 сохраняет свой вид при заглублении под поверхность. Именно это и показывают «сырые», нескорректированные данные измерений. Чтобы не афишировать эти убийственные для закона всемирного тяготения факты, авторы публикаций о тяготении в шахтах придерживаются следующих правил: 1) приводить данные лишь для уровней ниже поверхности, но не выше – чтобы не бросалось в глаза отсутствие «излома»; 2) не уточнять – увеличивается или уменьшается сила тяжести при погружении под поверхность; 3) не приводить «сырых» данных: приводить только данные, которые скорректированы хотя бы на действие поверхностных масс (а эти коррекции являются произволом: они зависят от принятой модели распределения поверхностных масс). При таких делах, почему же мы уверены в том, что в шахтах подтверждается не закон всемирного тяготения, а наша модель? Да повезло, знаете. Авторы статьи [С6], проводившие измерения в шахтах Квинсленда (Австралия), опубликовали-таки «сырые» данные (Табл.1, колонка 3). Причём, чётко указали, что представлены значения, измеренные на глубине, минус значение, измеренное на поверхности – откуда сразу ясно, что ускорение свободного падения увеличивается при погружении, а не уменьшается, как требует закон всемирного тяготения. Более того! Обратите внимание: согласно этому закону, модуль производной у высотной зависимости ускорения свободного падения при подходе к точке излома сверху, 2GMЗ/R3, в два раза больше чем при подходе к точке излома снизу, GMЗ/R3. При задействованном перепаде глубин ?h=948.16 м [С6], расчётная величина приращения ускорения свободного падения 2GMЗ?h/R3, т.е. при надповерхностном значении производной, составляет ?2.96?10-3 м/с2. Сравните с ней измеренное значение для названного перепада глубин: 2.9274?10-3 м/с2 [С6]. Совершенно очевидно: при переходе через поверхность Земли сверху вниз, не имеет место не только смена знака, но и двукратное уменьшение модуля производной у высотной зависимости ускорения свободного падения. Такое возможно, если всё вещество Земли не обладает притягивающим действием! Мы обнаруживаем здесь, прямо скажем, глобальный прокол закона всемирного тяготения – наша же модель подтверждается и качественно, и количественно. Знаете, один писатель, приближённый к военным кругам, красочно описывал, как наши атомные подводные лодки легко отрывались от американских, закладывая лихие виражи между подводных гор Срединно-Атлантического хребта. Это, якобы, потому, что на наших лодках были гравитационные детекторы подводных гор, а у американцев такой прелести не было. Ну, ну. Знал бы этот писатель о положении дел в гравиразведке полезных ископаемых. Практикам-то известно, что, несмотря на хорошо разработанную теорию, эффективность гравиразведки является наихудшей по сравнению с эффективностями других методик – например, сейсмической или электромагнитной. Показания гравиметров и вариометров (приборов на основе крутильных весов) лишь в ничтожном проценте случаев отражают истинную картину залегания тех или иных пород. И эти редкие случаи происходят просто потому, что если прибор указывает направление совершенно случайно, то рано или поздно он укажет его правильно. Неужто нашёлся бы капитан подводной лодки, который доверял бы подобным приборам? Или, пардон, на подводных лодках гравитационные детекторы – какие-то особенные? Основанные на том, что «в боевой обстановке значение синуса может приближаться к четырём»! Эх, а ведь до сих пор разные организации предлагают простакам услуги по гравиметрической разведке. Разведка пешая! Автомобильная! С борта самолёта! Со спутников! «Любые фантазии клиентов – за их денежки!» Причём, ведь гравиметрические карты рисуют – разноцветные! Ну, что тут скажешь. Во-первых, красиво. А, во-вторых, кому эти картинки мешают? 2.5. Где же притягивающее действие у малых тел Солнечной системы? В Солнечной системе собственное тяготение с полной очевидностью имеется у Солнца, планет и Луны; а также, если судить по наличию атмосферы, у Титана. Что касается остальных спутников планет, то мы обнаруживаем следующее. Во-первых, даже в случаях самых крупных спутников (в том числе и Титана) не обнаружена динамическая реакция их планет – которые, в согласии с законом всемирного тяготения, должны обращаться вокруг общего со спутником центра масс. Во-вторых, о тяготении спутников планет свидетельствовало бы наличие у них атмосфер. Но, за исключением Титана, явных признаков атмосфер ни у кого из них не обнаружено. В-третьих, ни у кого из шести десятков известных на сегодня спутников планет не обнаружено ни одного собственного спутничка. В свете теории вероятностей, такое положение вещей выглядит довольно-таки странным. В-четвёртых, особого упоминания заслуживают т.н. динамические определения масс спутников, основанные на аксиоме о том, что спутники одной планеты непременно возмущают движение друг друга. Если в действительности спутники не притягивают друг друга, то динамические определения их масс являются попытками решения некорректно поставленной задачи. И признаки этого – действительно налицо: результаты применения этой методики оказываются расплывчатыми и неоднозначными. Вот комментарии определения де Ситтером масс четвёрки крупных спутников Юпитера, на основе полученного им периодического решения: «Фактические орбиты спутников не соответствуют в точности периодическому решению, но могут быть получены из периодического решения вариацией координат и компонент скорости…», и далее: «…трудностью является медленная сходимость аналитического разложения по степеням масс» [М2]. Тем не менее, значения масс, «данные де Ситтером, следует считать наилучшими… Всякое уточнение этих значений потребовало бы построения новой теории, …потребовался бы также новый ряд наблюдений положений этих спутников» [Д1]. Выбранные здесь «наиболее вероятные» значения масс спутников – из набора не повторяющихся значений – едва ли могут служить доказательством того, что спутники действительно притягивают друг друга. Скорее, мы имеем свидетельство о том, что притягивающего действия у них как раз нет. Такое положение с собственным тяготением у спутников планет является тревожным, поэтому нас пытаются убедить в том, что признаки собственного тяготения имеются хотя бы у астероидов. «Смотрите, - показывали нам фотографии, - на поверхности астероида лежат валуны!» Но мы присматривались и обнаруживали, что эти валуны не «лежат» на поверхности, они вплавлены в неё. «Смотрите, - показывали нам другие фотографии, - на поверхности астероида видны озёра пыли!» Но пыль – если там действительно пыль – может держаться, например, на электростатике… Вот если у астероида обнаружился бы обращающийся вокруг него спутничек – это было бы похоже на доказательство наличия у астероида собственного тяготения. Ой, до чего же исследователям хотелось обнаружить такие спутнички! Для их визуального обнаружения, у наземных оптических телескопов было недостаточно хороша разрешающая сила, поэтому приходилось выкручиваться. Отыщут астероид с переменным блеском и заявят: это из-за того, что спутничек его периодически затмевает. Да нет, говорят им, это один астероид, просто он вращается и блестит то тёмной, то светлой гранями. Тогда отыщут астероид с двойной периодичностью кривой блеска: уж тут-то точно спутничек затмевает! Да нет, говорят им, это опять один астероид, только с асимметричной формой – например, с выростом – и он испытывает два вращения сразу. Тогда предъявят радио-изображения тесной парочки: допплеровские сдвиги свидетельствуют о её вращении около общего центра [П1]! Да нет, говорят им, это опять вращается один астероид, с перемычкой – радио-изображения и допплеровские сдвиги будут такие же. Неизвестно, сколько бы ещё длилась эта сказка про белого бычка, если бы не дальний космический зонд ГАЛИЛЕО. 28 августа 1993 года, пролетая рядом с астероидом Ида, этот зонд сделал серию его снимков, которые затем передал по радиоканалу на Землю. Оказалось, что на этих снимках запечатлён небольшой объект рядом с Идой; его назвали Дактилем. Если бы этот фотосеанс длился достаточно долго для того, чтобы зафиксировать обращение Дактиля вокруг Иды, то открытие спутника у астероида не вызывало бы сомнений. Но, увы, за короткое время пролёта зонда взаимное положение Иды и Дактиля, практически, не изменилось. При том, что масса Иды не была известна, реконструкция орбиты Дактиля, на основе закона всемирного тяготения, допускала весьма значительную неопределённость. Это не мы придумали, это они сами пишут: «Почти сразу стало ясно, что массу/плотность Иды не получить вместе с определением орбиты Дактиля. Вместо этого, был сконструирован набор его орбит – для различных возможных значений массы/плотности Иды, от 1.5 до 4.0 г/см3. Для различных значений плотности различны и орбиты, причём, для названного диапазона плотностей, орбиты различаются очень сильно. При плотностях Иды, меньших примерно 2.1 г/см3, орбиты оказываются всего лишь гиперболическими. При больших плотностях Иды орбиты являются эллиптическими с огромными удалениями в апоцентрах, с удалениями в перицентрах примерно 80-85 км, и с периодами, различающимися от примерно одних суток до многих десятков суток. При плотности примерно 2.8 г/см3, орбита почти круговая… с периодом около 27 часов. Для ещё больших плотностей, эллиптические орбиты имеют удаления в апоцентрах 95-100 км, а удаления в перицентрах уменьшаются с увеличением плотности. Для плотности Иды более чем 2.9 г/см3, удаление в перицентре меньше 75 км и период меньше 24 часов…» [ВЕБ1] (перевод наш). Давайте же смотреть правде в глаза: доказательства того, что Дактиль действительно обращался вокруг Иды – отсутствуют, как отсутствуют и доказательства того, что Ида оказывала на движение Дактиля хоть какое-то воздействие. Несмотря на, мягко говоря, сомнительность «первого достоверного» открытия спутника у астероида, из этого события сделали целую сенсацию. Ну, понятно: общественности не полагается знать, что учёные мужи, на переднем крае науки и техники, фигнёй страдают. Общественности полагается радоваться великим свершениям! А больше всех обрадовались астрономы, которые как раз вводили в строй новейшие астрооптические инструменты – телескопы с адаптивной оптикой. Это – редкостная прелесть. У обычных телескопов разрешение ограничено помехами, которые дают подвижки воздуха: абсолютно спокойной атмосферы не бывает. А при работе адаптивной оптики, все подвижки изображения в рабочем поле компенсируются и, с помощью компьютерной обработки, исключаются из результирующей картинки. То есть, ведёте вы таким телескопом какой-нибудь астероид (особенно хорошо, если он сам не вращается), и получаете его чёткий образ, а всё остальное – начисто отсекается! Причём, отсекаются не только шумы из-за подвижек воздуха – отсекается и звёздное небо, на фоне которого астероид летит. Автоматика – она же тупая! На снимках, сделанных с помощью обычных телескопов, звездное небо присутствует – что может худо-бедно свидетельствовать о том, что астроном не спал в ту самую ночь. А смотришь на эти «адаптивные» картинки – и недоумеваешь: а не состряпаны ли они, по-простому, средствами компьютерной анимации? Ведь никто не проконтролирует! Так вот, с помощью этой модерновой техники, астрономы кинулись выдавать «убедительные свидетельства» о наличии спутников у астероидов. Но, при ознакомлении с доступными сообщениями на эту тему, создаётся впечатление, что, включившись в «охоту за двойными астероидами», исследователи торопились делать свои приоритетные заявления, откладывая их надёжное обоснование «на потом». Если на интервале в несколько ночей воспроизводился образ объекта на небольшом угловом расстоянии от астероида, то объект классифицировался как спутник. В сообщениях не приводились доказательства того, что этот «спутник» действительно обращался вокруг астероида, и для параметров орбиты «спутника» давались, в лучшем случае, «предварительные оценки». Причём, эти так называемые оценки делались на основе минимального числа изображений. Лишь в единичных случаях сообщалось всего о трёх (!) взаимных положениях компаньонов [ВЕБ2], в большинстве же случаев обходились даже без этого [ВЕБ3-ВЕБ6]. Но ведь, при таких делах, параметры орбиты определить невозможно! Откуда же взялись значения периодов обращения спутников соответствующих астероидов, приведённые, например, в обзоре [ВЕБ7]? Для каждой из этих цифр следовало бы указать первоисточник, но этого не сделано. Впрочем, автора винить не следует: взгляните на официальный список параметров двойных астероидов, в том числе и параметров орбит их спутников [ВЕБ8]. Этот список сопровождается многочисленными ссылками, но эти ссылки – в никуда. Изучая их, нам так и не удалось прояснить происхождение приводимых цифр! Придётся нам констатировать, что список имеющих спутники астероидов – на конец 2005 г. их насчитывалось около семи десятков – составлялся на основе необоснованных заявлений. То, что есть парочки астероидов, которые просто летят рядом – это мы не оспариваем. Но не следует привирать, что эти парочки обращаются около общего центра масс! Ибо доказательств такого обращения – нету. Значит, нет доказательств и того, что астероиды имеют собственное тяготение – способное удерживать естественные спутнички. Но нас пытаются убедить в том, что уже дважды на орбиту вокруг астероида успешно выводились космические аппараты! Уж тут-то, мол, всё было без дураков! И что же мы видим? Первым, без дураков, был американский зонд NEAR, который подогнали близко к астероиду Эрос – с вектором скорости, мало отличавшимся от вектора скорости Эроса на его околосолнечной орбите. Всё было сделано идеально для того, чтобы зонд захватился тяготением астероида и стал его искусственным спутником. «Так и вышло!» - уверяют нас. Ой ли? А зачем же – после этого захвата – на протяжении всего времени, пока NEAR летал около Эроса, требовалось огромное количество незапланированных включений двигателя? Нам об этом известно потому, что ныне ход научных космических миссий освещается в реальном времени на официальных сайтах космических агентств и обсуждается на специализированных интернет-форумах. «Двигатель включался для коррекций орбиты» - поясняли специалисты из NASA. «Коррекции орбиты «посыпались» одна за другой» - вторили им комментаторы на портале «Новости космонавтики» [ВЕБ9]. Странная потребность во множестве незапланированных коррекций орбиты для успешного хода миссии настолько бросалась в глаза, что по ходу дела американцам пришлось придумывать объяснение происходящему. Судя по материалам того же источника [ВЕБ9], таких объяснений придумали аж два. Согласно первому, множественные незапланированные коррекции орбиты потребовались для того, чтобы зонд, со своими солнечными батареями, поменьше находился в тени. Но отсюда прямо следовало, что, при разработке проекта, орбиту зонда рассчитывали идиоты – а другие идиоты всё это утвердили. Поэтому выдвинули вторую версию. Оказывается, команде управленцев полётом пришлось иметь дело с двумя группами учёных, научные интересы которых расходились в вопросе о желательном удалении зонда от поверхности астероида – оттого-то, якобы, управленцы всё время были вынуждены то уводить зонд подальше от астероида, то, наоборот, подводить поближе к нему. Мол, это всё из-за учёных – что на протяжении года зонду не дали сделать ни одного полного витка по нормальной кеплеровой траектории! А откуда мы это знаем? Да мы ещё не совсем забыли, чему нас учили в школе: сразу после одного-двух таких нормальных витков можно было вычислить массу Эроса! И не нужно быть пророком, чтобы быть уверенным: быстрое определение массы Эроса было запланированной сенсацией. Ну, не сумасшедшие же рулили зондом NEAR! На орбиту, его, значит, вывели – дальше просто немного подождите, пока он сделает виток, и масса Эроса у вас на блюдечке! Но нет – ученые, мол, этого не допустили. Пришлось идти у них на поводу и постоянно корректировать орбиту! Театр абсурда какой-то! Но в этом театре абсурда всё моментально проясняется, если иметь в виду, что собственного тяготения у астероида Эроса нет – а, значит, и никакого захвата зонда этим тяготением не было. Однако, надо же было удерживать зонд рядом с астероидом – вот и приходилось незапланированно включать двигатель, чтобы изменять направление дрейфа зонда около астероида. Так и гоняли зонд по кусочно-ломаной траектории вокруг астероида – в течение года! Это и называлось у них «успешным выводом на орбиту». Да, но ведь запасы рабочего вещества для ионного движка зонда со временем должны закончиться? Именно! Нехорошо получится. Ведь планировалось так и оставить зонд на орбите вокруг Эроса – чтобы надолго сохранилось свидетельство о выдающемся научно-техническом достижении. А зонд, после прекращения «коррекций орбиты», возьмёт да уйдёт от астероида! Выяснится, чего доброго, что никакой орбиты-то не было, и что руководители проекта дурачили общественность. Вот и решили: когда запасы рабочего вещества подойдут к концу, надо будет грохнуть зонд о поверхность астероида – называя это попыткой мягкой посадки. Непосвящённых привела в восторг смелость этого решения, ведь «к посадке зонд был совершенно не приспособлен»! Кстати, как делать «посадку» на объект, не имеющий собственного тяготения? Это делалось впервые в истории! Здесь не требуется традиционный тормозной манёвр на орбите: нужно направиться прямо на объект – и, перед столкновением, притормозить. Или – не притормозить, понимаете? В общем, посадка вышла та, что надо: грохнутый об поверхность зонд подавал признаки жизни ещё в течение месяца… Повторяем, все эти события обсуждались в реальном времени на форумах – где специалисты мемекали и бебекали, не находя разумных объяснений творившемуся абсурду. Но, спустя некоторое время, умники из NASA переписали историю – самое главное, выдали официальный протокол: «полный» список коррекций орбиты NEAR. Причём, для каждой коррекции обнародовали все интимные подробности – и обоснование, и параметры, и дату-время. Это они вот зачем: вдруг кто-нибудь лет через десять возбухнет – а зачем вы, мол, включали двигатель не по делу? Так тогда его – мордой в этот протокол! Всё, мол, было по делу, недоумок! Был, мол, типичный орбитальный полёт! Знаете, каков был главный источник проблем в миссии NEAR? А он был таков: двигатель зонда включался командами с Земли! О каждом включении знало слишком много народу, вот и пришлось отдуваться за незапланированные «коррекции орбиты». Хитрые японцы устранили эту проблему напрочь: их зонд HAYABUSA, который они отправили к астероиду Итокава, был «оснащён автономной системой навигации, которая позволяет ему сближаться с астероидами в полностью автоматическом режиме, без участия наземных операторов» [ВЕБ10]. При этом проблемы с удержанием зонда вблизи астероида не слишком бросались в глаза, и основные усилия японцы сосредоточили на выполнении научной программы. В частности, планировалось высадить на Итокаву исследовательский робот, который, после отделения от зонда на положенной высоте, должен был очень медленно упасть на поверхность. Но… не упал. «Микроробот «Минерва»… успешно стартовал с зонда «Хаябуса» в субботу, 12 ноября 2005г., но вскоре начал удаляться от астероида» [ВЕБ11]. Так и уплыл он в космические дали. Странным образом, это не поколебало уверенность специалистов в том, что у астероида имеется собственное тяготение. Действуя вполне последовательно, они отправили на поверхность астероида ещё одну болваночку без двигателей – отражающий шарик, который должен был выполнять роль навигационного маркера при работе лазерных дальномеров, обеспечивающих посадку на астероид самого зонда, для взятия пробы грунта. Когда дело дошло до работы лазерных дальномеров… ну, в общем, выяснилось, что шарика-отражателя нет на положенном месте. Куда он мог деться, если его аккуратно сбросили с высоты всего в 40 метров [ВЕБ30], и ему оставалось лишь опуститься на поверхность, двигаясь с мизерным ускорением? И это был уже второй прокол подряд! И второй раз подряд японцам пришлось давать смехотворные, наскоро состряпанные объяснения [Г17]! Но здесь уже не выдержали журналисты. Они обрушились на руководителей проекта с требованием, чтобы вторая попытка посадки зонда на поверхность астероида освещалась в прямом эфире. Неслыханная наглость, правда? Но уж так был крепок маразм происходящего, что пришлось японцам согласиться на прямой эфир. Правда, в этом прямом эфире, по ходу второй попытки посадки, связь с зондом на самом интересном месте прервалась. Как по заказу! Так что сел ли японский зонд на астероид, и взял ли он там пробу грунта – науке неизвестно. После этого, массовый интерес к зонду HAYABUSA угас, и мало-помалу страсти улеглись. Спустя год, провели даже научную конференцию по тематике HAYABUSA-Итокава. Среди всего прочего, там демонстрировалась гравиметрическая карта астероида. Сам видел – редкой красоты вещь! Выполнена в традициях дзен; оказывает успокаивающее и расслабляющее действие. Созерцая этот шедевр, ни за что не подумаешь, что болванки без движков рядом с астероидом не удерживались! 2.6. Малые планеты: как же они ускоряются к Солнцу? Из закона всемирного тяготения следует, что притяжение к нескольким массивным телам равно векторной сумме притяжений к каждому из них по отдельности. Т.е., тяготения нескольких тел действуют совместно, аддитивно. Такой подход приводит к поразительному парадоксу; мы изложим его в терминах гравитационных потенциалов. Тело, имеющее собственное тяготение, находится в центре своей потенциальной ямы. Быть в яме означает быть в устойчивом равновесии. Отчего же малое тело, находясь вблизи много большего тела, ускоряется к нему? Оттого, говорят нам, что потенциальная ямка малого тела, складываясь с потенциальным склоном большого тела, возмущает этот склон настолько слабо, что суммарное распределение потенциала в объёме малого тела представляет собой, в первом приближении, склон, а не ямку – а по склону тело должно «скатываться». Очень хорошо! Теперь пусть малое тело удаляется всё дальше от большого. При этом крутизна потенциального склона большого тела становится всё меньше, и, наконец, она сравняется с крутизной потенциальной ямки малого тела на его поверхности. Расстояние от большого тела, на котором это произойдёт, мы называем дальностью отчуждения. За пределами дальности отчуждения малое тело находится уже не «на склоне», а «в ямке». Конечно, эта «ямка» асимметрична из-за перекоса, наводимого склоном большого тела – но теперь это, в первом приближении, ямка, а не склон. А в ямке тело должно удерживаться. С чего ему теперь «скатываться» в сторону большого тела? В перекошенной ямке у тела будет другое положение равновесия и другое распределение деформаций, чем в симметричной ямке, но перекошенная ямка будет удерживать тело не хуже, чем симметричная. Таким образом, из универсальности действия тяготения следует вывод: малое тело, находящееся за пределами дальности отчуждения от большого тела, не должно к нему ускоряться. Но практика не подтверждает этот вывод. Действительно, для малого тела с массой m и радиусом r, дальность отчуждения Dот от большого тела с массой M есть
В таблице приведены рассчитанные по этой формуле дальности отчуждения от Солнца для некоторых малых планет (a – расстояние от Солнца в афелии; справочные данные взяты из [К2]).  Как можно видеть, расстояния от Солнца, на которых малые планеты, несомненно, ускоряются к нему, на порядок превосходят соответствующие дальности отчуждения. Как такое возможно? Парадокс легко разрешался бы, если у малых планет, действительно, не было бы собственного тяготения, т.е. не было бы своих потенциальных ямочек. Тогда для них не было бы и дальностей отчуждения от Солнца, и они могли бы ускоряться к нему в пределах всей области действия солнечного тяготения – что и происходит в действительности. 2.7. Частотные склоны, как причина тяготения. Скорость действия тяготения. Выше мы привели ряд примеров, которые свидетельствуют о том, что вещество не обладает способностью порождать тяготение. Оно не притягивает, оно лишь подчиняется тяготению. К чему же оно тяготеет? В такой форме – «К чему?» - вопрос некорректен. Правильнее спросить: «Куда направлено силовое воздействие?» Тогда ответ таков: «Оно направлено вниз по местной вертикали». А эти местные вертикали заданы чисто программными средствами. Как мы излагали в 1.6, частоты квантовых пульсаций заданы программно. Если частота квантовых пульсаций, например, электрона, была бы задана одинаковой во всём пространстве, то такое пространство было бы «плоское», и в таком мире не было бы тяготения. Но программы, порождающие тяготение, обязывают частоты квантовых пульсаторов зависеть от местоположения в пространстве. Таким образом формируется программная реальность, которую мы называем частотными склонами. В области пространства, в которой «действует» частотный склон, в каждом месте задан локальный градиент частот квантовых пульсаций. Таким образом, в объёме пробного тела, находящегося на частотном склоне, программно формируется градиент частот квантовых пульсаций. К чему это приводит? Как отмечалось в (1.4), частота квантового пульсатора и его собственная энергия прямо пропорциональны друг другу. Следовательно, градиент этих частот означает градиент энергий. А градиент энергий означает силовое воздействие. Действительно, теоретическая механика учит, что вектор силы, действующей на тело, пропорционален и противоположно направлен градиенту потенциальной энергии – отчего тело, находящееся на склоне потенциальной ямы, «скатывается вниз». Но потенциальная энергия тела не вписывается в реалии «цифрового» мира. Эта энергия зависит только от местоположения тела и не соответствует никакой форме движения – тогда как такое соответствие является непременным атрибутом реальной физической энергии (1.3). Такой реальной энергией является энергия квантовых пульсаций, и тяготение организовано через градиенты именно этой энергии – через частотные склоны. Находясь на частотном склоне, пробное тело испытывает силовое воздействие, направленное «вниз», т.е. туда, где частоты квантовых пульсаций меньше. При этом ускорение свободного падения, сообщаемое пробному телу локальным участком частотного склона, есть [Г5]
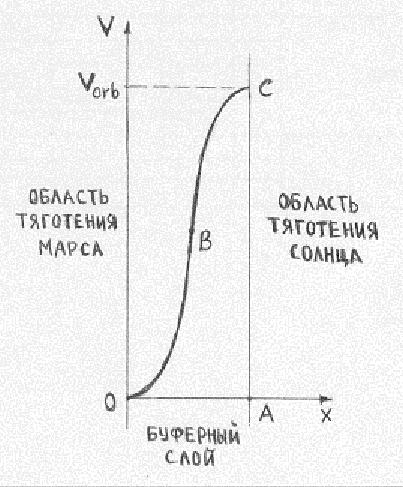
где df/dr – локальный градиент частот, c – скорость света. О чём говорит это выражение? Прежде всего, оно подчёркивает непричастность масс к порождению тяготения, поскольку, как можно видеть, ускорение свободного падения не зависит от массы «силового притягивающего центра»: оно определяется лишь геометрией локального участка частотного склона. Далее, из выражения (2.7.1) тривиально следует объяснение того факта, что, скажем, в одном и том же месте области действия тяготения Земли, различные тела имеют одно и то же ускорение свободного падения – независимо от их массы, формы, химического состава и агрегатного состояния. Эйнштейн придавал этому факту фундаментальное значение. Он полагал, что его теория объяснила этот фундаментальный факт. Там вышло вот что: в ньютоновском законе всемирного тяготения фигурирует т.н. гравитационная масса тела, а в выражении второго закона Ньютона – его инертная масса. Комбинация этих выражений даёт, что ускорение свободного падения тела прямо пропорционально отношению его гравитационной массы к инертной. А это отношение в каждом месте одинаково для различных малых тел – и пусть оно, мол, равно единице! Тогда, мол, всё сходится! Но у этого «объяснения» есть всего один недостаточек. Оно, может, и работало бы, если понятие «гравитационная масса» имело бы физический смысл – если массы обладали бы притягивающим действием. Но, как проиллюстрировано выше, это не так. А одинаковость ускорения свободного падения у разных тел обусловлена тем, что в любом месте крутизна частотного склона, порождающего тяготение, одинакова для всех. Поэтому, когда говорят, что эксперименты Этвёша, Дикке и Брагинского установили равенство инертной и гравитационной масс с точностью аж до двенадцатого знака, то надо понимать, что установили-то, с этой точностью, одинаковость ускорений свободного падения для различных тел, и ничего сверх этого. Согласно (2.7.1), идентичность этих ускорений, сообщаемых разным малым телам одним и тем же участком частотного склона – это по определению так. Не нужно здесь изображать заумную «фундаментальность»! Ещё одно следствие из выражения (2.7.1) таково: на пробное тело действует не удалённый «силовой центр», а локальный градиент частот – поэтому тяготение действует без задержки во времени. Этот вывод несовместим с декларацией общей теории относительности о том, что «скорость действия тяготения очень велика, но больше скорости света она быть не может – значит, она равна скорости света». В насмешку над подобными декларациями, имеются надёжные экспериментальные факты, которые свидетельствуют о действии тяготения без задержки во времени. Так, Ван Фландерн обращает внимание на тот факт, что в уравнениях небесной механики скорость действия тяготения однозначно принимается бесконечной [Ф1], и, именно при этом, движение небесных тел описывается с огромной точностью – с погрешностями до нескольких угловых секунд за столетие. Если скорость действия тяготения была бы конечна, и на планету действовала бы сила тяготения, соответствующая не мгновенному положению планеты, а её некоторому предшествовавшему положению, то эта сила действовала бы нецентрально. Тогда орбиты планет эволюционировали бы, увеличивая свои средние радиусы – но ничего подобного не наблюдается. Исходя из этого, ещё Лаплас, основываясь на доступных ему данных астрономических наблюдений, сделал вывод о том, что нижнее ограничение на скорость действия тяготения превышает скорость света на 7 порядков [Л2]. Ещё более впечатляющие цифры получены уже в нашу эпоху – по результатам приёма импульсов пульсаров, расположенных на различных участках небесной сферы. На основе совместной пост-обработки последовательностей этих импульсов, находили текущий вектор скорости Земли, а затем, беря производную этого вектора по времени, находили текущий вектор ускорения Земли. Оказалось, что компонента этого вектора, обеспечивающая центростремительное ускорение Земли при её орбитальном движении, всегда направлена не к мгновенному видимому положению Солнца, а к его мгновенному истинному положению. Поперечный сдвиг «оптического Солнца», из-за задержки на распространение света, обнаруживается, а поперечный сдвиг «гравитационного Солнца», из-за запаздывания действия тяготения – не обнаруживается. В итоге Ван Фландерн сообщил о нижнем ограничении на скорость действия тяготения, которое превышает скорость света уже на 10 порядков [Ф1]. В этой связи нельзя не упомянуть про нашумевший эксперимент Копейкина-Фомалонта, которые заявили, что измерили «скорость гравитации» - наблюдая, с помощью нескольких радиотелескопов, сдвиг радиоизображения квазара при близком прохождении Юпитера. Авторы утверждали, что они обнаружили совпадение скорости гравитации со скоростью света в пределах точности 20% [К3,К4]. Свой результат они представили как «первое измерение скорости гравитации», как будто не было результатов ни Лапласа, ни Ван Фландерна. В статье [Г6] мы дали подробный анализ того, что делали Копейкин и Фомалонт. Мы обнаружили, что заявленный ими результат основан на сознательной имитации желаемого эффекта. Этим результатом ничуть не опровергается вывод о действии тяготения без запаздывания во времени – что находится в согласии с вышеназванными экспериментальными реалиями. Здесь уместно упомянуть о весьма драматической, по своим смехотворным результатам, области физического эксперимента – ловле гравитационных волн. На что ловцы гравитационных волн надеялись, с завидным упорством строя свои детекторы в расчёте на то, что скорость этих волн равна скорости света? Неужто они надеялись на то, что сегодня мало кто знаком с трудами Лапласа? Но вернёмся к выражению (2.7.1) и заметим, что оно даёт математически верное значение для крутизны частотного склона – это подтверждается опытом. Крутизна околоземного частотного склона была впервые измерена, с помощью мёссбауэровской спектроскопии, в 1959 г. Паундом и Ребкой [П2]. Правда, они неверно интерпретировали свой результат – полагая, что измерили «гравитационное красное смещение», т.е. гравитационный сдвиг частоты у гамма-квантов, движущихся вертикально. Они не приняли во внимание, что если источник и поглотитель находятся на разных высотах, то их спектральные линии имеют тот же самый взаимный гравитационный сдвиг [Л3]. Если ещё и гамма-кванты, при своём вертикальном движении, изменяли бы свою частоту, то итоговый эффект был бы удвоенный – а он был одинарный. Строго говоря, схема эксперимента Паунда и Ребки не позволяла сделать вывод об источнике обнаруженного эффекта: является ли он следствием взаимного сдвига линий источника и поглотителя, или следствием сдвига частоты гамма-квантов, движущихся по вертикали. Но в дальнейшем был проведен целый ряд экспериментов с перевозимыми атомными часами, в частности, многочисленные применения этих часов на бортах ИСЗ. Эти эксперименты убеждают нас в том, что гравитационные сдвиги квантовых уровней энергии в веществе непременно имеют место – причём, они в точности объясняют и результат Паунда и Ребки. Значит, эти авторы измерили не сдвиг частоты у гамма-квантов, а именно крутизну околоземного частотного склона. Действительно, при 22.5-метровой разнице высот расположения мёссбауэровских источника и поглотителя, относительная разность частот составила около 2.5?10-15. Отношение второй из этих величин к первой, умноженное, согласно (2.7.1), на квадрат скорости света, даёт значение ускорения свободного падения на поверхности Земли. Наконец, заметим, что локальный градиент частот (2.7.1) не только задаёт направление, в котором пробное тело приобретает ускорение свободного падения – градиент частот (2.7.1) обеспечивает также превращения энергии при свободном падении. При перемещении пробного тела вниз по местной вертикали, уменьшаются частоты его квантовых пульсаторов, т.е. уменьшается его масса, или собственная энергия. Эта убыль собственной энергии пробного тела идёт на приращение его кинетической энергии – чем энергетически обеспечено приобретение пробным телом ускорения свободного падения [Н1,Г7]. Чем круче частотный склон, тем больше величина этого ускорения (2.7.1). 2.8. Планетарные частотные воронки. Унитарное действие тяготения. Совокупность окружающих планету частотных склонов представляет собой сферически-симметричную частотную яму, в центре которой удерживается планета. Геометрия этой частотной ямы такова, что для силы тяготения, действующей на малое пробное тело, имитируется известный закон обратных квадратов. Совокупность частотных склонов, порождающих планетарное тяготение, мы называем планетарной частотной воронкой. Будучи встроены в частотные склоны Солнца, планетарные частотные воронки имеют конечные размеры и выраженные границы (1.10, 1.11), за которыми – т.е. в межпланетном пространстве, не занятом частотными воронками планет – действует только солнечное тяготение. Даже если солнечное тяготение действовало бы и в пределах планетарных частотных воронок, складываясь там с планетарным тяготением, то их совместное действие не могло бы обеспечить центростремительного ускорения планеты к Солнцу. По аналогии с изложенным в 2.6, участок солнечный склона, приходящийся на планетарную воронку, деформировал бы её – отчего возникало бы направленное к Солнцу воздействие на вещество планеты. Но ведь планета продолжала бы оставаться в деформированной воронке. Значит, если даже солнечный склон навёл бы «перекос» этой воронки, планета всего лишь заняла бы в ней новое положение равновесия – но центростремительного ускорения к Солнцу планета не имела бы, если его не имела бы сама планетарная частотная воронка [Г4]. А это уже очень интересно. Это приоткрывает тайну происхождения Солнечной системы. Ни одна из выдвинутых на эту тему научных гипотез, основанных на законе всемирного тяготения, не проясняет главного: каким это дивным образом планеты в своё время приобретали «правильные» векторы скорости, чтобы продолжать своё движение по, практически, круговым орбитам, радиусы которых зависят от их порядкового номера, подчиняясь эмпирическому правилу Тициуса-Боде [С3]. Мы же, с учетом вышеизложенного, приходим к выводу об искусственном устроении движения планет. Вещество планет просто удерживается в центрах планетарных частотных воронок – для которых организовано орбитальное движение вокруг Солнца. Организовано, конечно, чисто программными средствами [Г4] – да так, чтобы для ускорений планетарных частотных воронок к Солнцу и друг к другу имитировался закон обратных квадратов (см. также 4.14)! И, в дополнение к этому чуду, имеются экспериментальные свидетельства о том, что в пределах планетарных частотных воронок, т.е. в областях действия планетарного тяготения, солнечное тяготение «отключено», т.е. планетарная частотная воронка не деформирована из-за наложения на неё соответствующего участка солнечного частотного склона. Так, убийственное свидетельство об «отключенности» солнечного тяготения в окрестностях Земли появилось с началом эры GPS. Если бы солнечное тяготение действовало здесь аддитивно с земным, то спутники GPS, движущиеся над дневной и ночной сторонами Земли, находились бы в неодинаковых гравитационных потенциалах. Соответственно, бортовые атомные часы на этих спутниках имели бы неодинаковые хода. Максимальная относительная разность этих ходов 2aSR/c2, где aS - ускорение свободного падения к Солнцу на радиусе орбиты Земли, R - радиус орбиты спутников GPS, c - скорость света, составляла бы величину около 3.5?10-12. Такие вариации ходов бортовых часов GPS, с периодом около полусуток, были бы быстро и уверенно обнаружены – но о них не сообщается. А ведь если эти вариации имели бы место, то их интерпретация – через аддитивное действие земного и солнечного тяготений – не заставила бы себя ждать. Почему же об этих вариациях помалкивают? Ответ очевиден: потому что их нет. А, значит, нет и никакого «аддитивного» действия планетарного и солнечного тяготения. Вместо этого, имеет место разграниченность областей действия солнечного и планетарных тяготений – малое пробное тело, где бы оно ни находилось, тяготеет либо только к планете, либо только к Солнцу (исключение – короткодействующее тяготение Луны, которое наложено на земное тяготение (2.12)). В организации действия тяготения по такому, унитарному, принципу мы усматриваем большой смысл. Вспомним, что превращения энергии в «цифровом» мире должны происходить однозначно (1.3). При свободном падении тела изменяется его кинетическая энергия, однозначное значение которой зависит от квадрата локально-абсолютной скорости тела. А эта скорость определяется по отношению к локальному участку частотного склона. Значит, для однозначности превращений энергии при свободном падении, пробное тело должно иметь одну локально-абсолютную скорость, т.е. находиться только на одном частотном склоне – а, значит, солнечные и планетарные частотные склоны не должны накладываться друг на друга. Организация тяготения по унитарному принципу радикально упрощает не только мироустройство, но и расчёты движения малого тела – например, космического аппарата при межпланетном полёте. В рамках традиционного подхода, задача движения аппарата при его притяжени к нескольким силовым центрам – даже всего к двум! – уже не имеет аналитического решения. Унитарное же действие тяготения устраняет эту проблему. Где бы ни находился аппарат, он притягивается к одному силовому центру – и его движение описывается аналитически. Практика межпланетных полётов с очевидностью это подтверждает (1.10)! С учётом вышеизложенного, происхождение планет нам представляется следующим образом. В солнечный частотный склон встраивали частотную воронку будущей планеты и приводили её в орбитальное движение вокруг Солнца, а затем в эту воронку «загружали» вещество, из которого формировалась планета. При такой технологии, в результате загрузки в готовую воронку даже крупнодисперсных глыб вещества, глобальная фигура формируемой планеты мало отличалась бы от шаровой (см. также 4.14). В этой связи, мы не можем обойти молчанием такую аномалию в устройстве Солнечной системы, как отсутствие планетарной частотной воронки на орбите между Марсом и Юпитером. Согласно вышеупомянутому правилу Тициуса-Боде, там должна обращаться ещё одна планета, но вместо неё там имеет место пояс астероидов. Происхождение этого пояса астероидов официальная наука затрудняется объяснить. Действительно, чтобы развалить на обломки «гравитирующую» планету, следовало бы «совершить работу против сил гравитации». Это мог бы сделать достаточно мощный взрыв, но тогда разные обломки приобрели бы приращения к вектору орбитальной скорости, сильно различающиеся по величинам и направлениям. Поэтому траектории орбит обломков планеты, образовавшихся в результате её взрыва, имели бы огромный разброс параметров – и никакого пояса астероидов не было бы. Чтобы образовался пояс астероидов из планеты, её вещество должно было тихо рассредоточиться. Мы усматриваем здесь единственный разумный сценарий: по какой-то причине, частотная воронка планеты была отключена (ясно, что если программными манипуляциями возможно частотную воронку создать, то уничтожить её – тоже возможно). При этом вещество планеты могло рассредоточиться в результате срабатывания одних лишь сил упругости, до этого уравновешивавших силы гравитационного сжатия. Что касается воззрений официальной науки на пояс астероидов, то она ухватилась за гипотезу о том, что астероиды – это строительный материал, из которого планета так и не сформировалась. Указывают даже причину такой неудачи: влияние, каким-то образом, сильного гравитационного поля Юпитера. Эта версия не выдерживает критики, если иметь в виду, что в Солнечной системе планетарные частотные воронки, а, значит, и области планетарного тяготения, не перекрываются друг с другом. Орбита пятой планеты недосягаема для области действия тяготения Юпитера, поэтому формированию пятой планеты Юпитер никак не мог помешать. В 2.10 мы проиллюстрируем это с особенной наглядностью. 2.9. Буферные слои на границах планетарных частотных воронок. Вопрос о том, как организованы границы, разделяющие области планетарного и солнечного тяготения, заслуживает отдельного разговора. Если планетарные и солнечный частотные склоны порождаются чисто программными средствами, то и толщину переходного слоя – разделяющего планетарную частотную воронку и солнечный частотный склон – можно было задать программными средствами. Мы обращаем внимание на то, что, при малости толщины переходного слоя, прохождение сквозь него физических тел сопровождалось бы серьёзными проблемами. Эти проблемы связаны с тем, что неодинаковость локально-абсолютных скоростей у различных элементарных объёмчиков тела, пересекающего переходный слой, порождала бы механические напряжения в теле – и, при достаточно малой толщине переходного слоя, эти напряжения могли бы разрушить тело. Проиллюстрируем это на примере влёта космического аппарата, запущенного с Земли, в область тяготения Марса. Энергетически наиболее выгодная траектория полёта к Марсу (т.н. гомановская, [Л4]) – это околосолнечный полуэллипс, с перигелием в области орбиты Земли и с афелием на орбите Марса. Гелиоцентрическая скорость аппарата, достигшего орбиты Марса, составляет при этом около 20 км/с, а орбитальная скорость Марса есть 24 км/с, и тогда влёт в марсианскую частотную воронку возможен лишь через переднюю полусферу её границы. Сразу после пересечения этой границы, планетоцентрическая скорость аппарата составит, по правилам векторного сложения [Л4], 4 км/с. Если толщина переходного слоя l была бы меньше, чем размер аппарата, то возникала бы ситуация, при которой части аппарата, находящиеся по внешнюю и по внутреннюю стороны переходного слоя, имели бы локально-абсолютные скорости, соответственно, V0=20 км/с и V1=4 км/с. Эквивалентное ускорение было бы равно a=(V02-V12)/2l. Так, при l=1 м, это ускорение составило бы чудовищную величину 2?108 м/с2, т.е. около 2?107 g! В такой ситуации, аппарат разнесло бы в пыль. Как нам представляется, для возможности более «мягкого» прохождения тел сквозь границу области планетарного тяготения, эта граница представляет собой довольно толстый буферный слой, на котором задано такое согласующее изменение локально-абсолютной скорости, чтобы результирующие механические напряжения были не слишком разрушительны. Сделаем оценку для толщины буферного слоя в центральной части передней полусферы частотной воронки Марса, которая обеспечивала бы пролёт объекта с
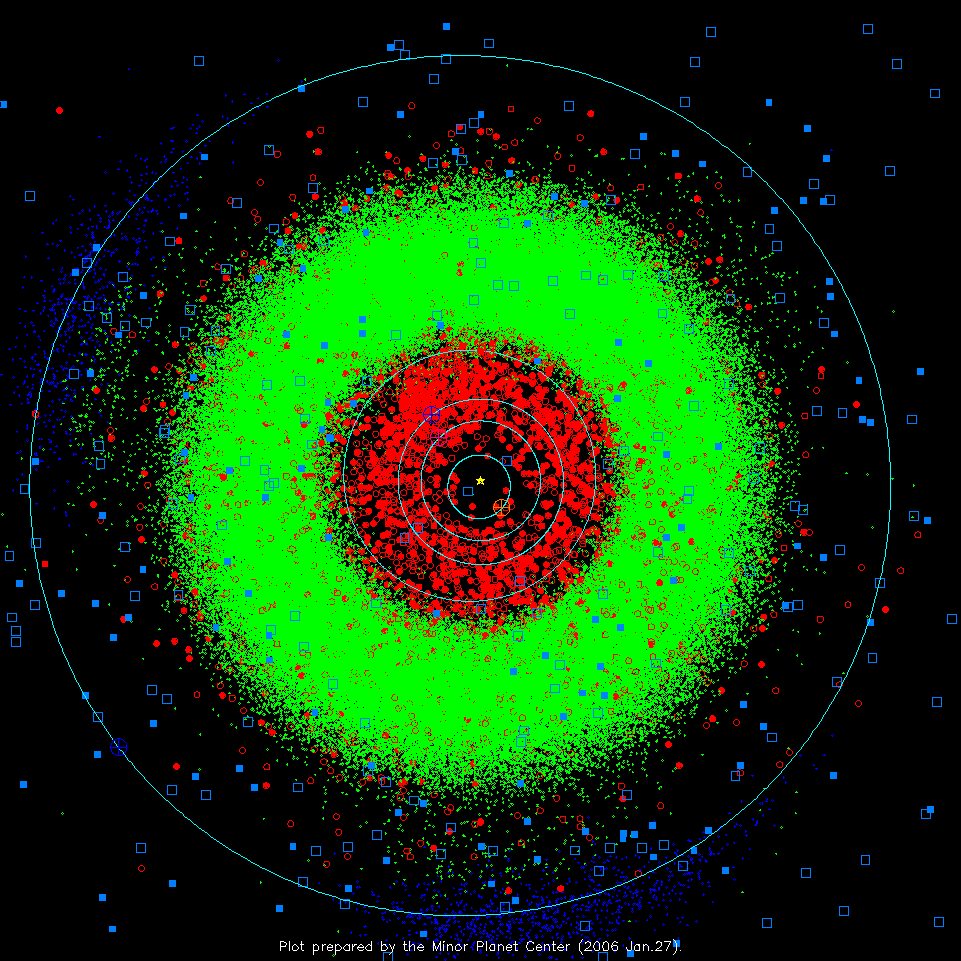
Рис.2.9 характерным размером L=100 м при механических напряжениях, соответствующих ускорению не более чем amax=5g. Полный размах приращения локально-абсолютной скорости на толщине буферного слоя должен равняться орбитальной скорости Марса, т.е. Vorb=24 км/с. Подчеркнём, что это приращение локально-абсолютной скорости, согласующее её значения по обе стороны от буферного слоя, возможно обеспечить лишь программными средствами! Пусть согласующая функция составлена из двух «встречных» ветвей одинаковых квадратичных парабол – ОВ и СВ (см. Рис.2.9). Здесь область отрицательных значений абсцисс соответствует области тяготения Марса, область абсцисс ОА соответствует буферному слою, область больших абсцисс – области солнечного тяготения. Наибольшая скорость изменения крутизны согласующей функции, приводящая к наибольшим механическим напряжениям в теле, приходится, очевидно, на центральную часть буферного слоя. Искомая результирующая толщина буферного слоя есть D= Vorb(2L/amax)1/2, для нашего случая она составляет около 84 км – что на четыре порядка меньше радиуса планетарной частотной воронки. Хотя этот результат выглядит правдоподобно, он имеет, конечно, исключительно ориентировочный характер. Заметим, что буферный слой на границе планетарной частотной воронки может защищать планету от крупных астероидов. Параметры буферного слоя могут быть заданы таким образом, чтобы достаточно крупные астероиды, влетающие в область планетарного тяготения, разрушались на более мелкие фрагменты. Не исключено, что дробление астероидов или комет, на влёте в область планетарного тяготения, является одним из сценариев, по которому образуются метеорные потоки в Солнечной системе. 2.10. Феномен астероидов-Троянцев. Имеется особое семейство астероидов, т.н. Троянцев. В него входят две группы, движущиеся примерно по орбите Юпитера и с таким же, как у Юпитера, периодом обращения вокруг Солнца, причём одна из этих групп опережает Юпитер примерно на 60о, а другая – на столько же отстаёт. Феномен Троянцев считается важным свидетельством справедливости закона всемирного тяготения – для частного случая задачи трёх тел. Ведь каждое из этих трёх тел, якобы, притягивает два других и, в свою очередь, притягивается ими. При таком подходе, аналитические решения найдены лишь для некоторых частных случаев, например, для случая, когда массы трёх тел сильно различаются и подчиняются соотношению M1>>M2>>M3. Лагранж показал, что должны существовать такие местонахождения тела M3 по отношению к паре M1 и M2, что все три тела будут обращаться вокруг общего центра масс с одной и той же угловой скоростью, и, таким образом, система при вращении будет сохранять свою конфигурацию. Лагранж предсказал пять таких особых местонахождений тела M3 по отношению к паре M1 и M2, эти местонахождения называются точками Лагранжа или точками либрации (см., например, [Л4]). Три из них, неустойчивые, находятся на прямой, проходящей через тела M1 и M2. Четвёртая и пятая точки либрации находятся в тех местах орбиты тела M2, которые равноудалены от тел M1 и M2; когда тело M3 находится в четвёртой или пятой точке либрации, положения трёх тел задают вершины равностороннего треугольника. Считается, что эти две точки либрации могут быть устойчивы [С4], и в окрестностях именно этих точек наблюдаются две группы Троянцев, если телом M1 считать Солнце, а телом M2 – Юпитер. Казалось бы, мы имеем дело с блестящим подтверждением традиционных воззрений на тяготение, согласно которым движение Троянцев определяется действием двух притягивающих центров: Солнца и Юпитера. Если бы это было действительно так, то один лишь феномен Троянцев делал бы негодной нашу модель унитарного действия тяготения – согласно которой, Троянцы находятся за пределами частотной воронки Юпитера, и поэтому они должны тяготеть только к Солнцу. Но мы постараемся показать, что как раз такой подход даёт более правдоподобное объяснение феномена Троянцев. Официальная теория гласит: вблизи устойчивой точки либрации «выведенное из равновесия» тело должно совершать эллиптические колебания вокруг этой точки [С4]. Каковы же размеры области устойчивости, в пределах которой возможны эти эллиптические колебания? По логике методов возмущений, отношение характерного размера области устойчивости к характерному расстоянию в данной задаче, т.е. к радиусу орбиты Юпитера, должно быть малым параметром, много меньшим единицы. В действительности же, разброс положений Троянцев грандиозен. На Рис.2.10 приведена карта положений малых тел Солнечной системы на 27 января 2006 г., в проекции на плоскость эклиптики; рисунок заимствован с общедоступного ресурса [ВЕБ12]. Здесь астероиды главного пояса обозначены малыми зелёными точками. Орбиту Юпитера изображает внешняя окружность; Юпитер, обозначенный кружком с крестиком, находится в точке, соответствующей примерно семи с половиной часам на циферблате; Троянцы изображены синими точками; центры их групп соответствуют примерно девяти с половиной и пяти с половиной часам. План выполнен с сохранением масштабов, и, как можно видеть, размеры «облаков» Троянцев сравнимы с радиусом орбиты Юпитера – вопреки теоретическим ожиданиям. Более того: чётко видно, что вытянутые вдоль орбиты Юпитера «облака» Троянцев изогнуты в соответствии с кривизной этой орбиты – словно, начиная с некоторой амплитуды, колебания Троянцев происходят по «изогнутым эллипсам»! Таким образом, модель колебаний Троянцев около устойчивых точек либрации приводит к абсурду. Ключом же к разумному объяснению феномена является факт совпадения периодов «колебаний» Троянцев с периодом обращения их и Юпитера вокруг
Рис.2.10 Солнца. Этот факт допускает совсем простую интерпретацию: Троянцы всего лишь движутся вокруг Солнца по эллиптическим орбитам с большими полуосями, равными большой полуоси орбиты Юпитера – тогда периоды их обращения такие же, как и у Юпитера. И ещё их орбиты имеют некоторый разброс по степени эллиптичности, т.е. разброс эксцентриситетов. Чем больше разница эксцентриситетов орбиты Троянца и орбиты Юпитера, тем больше размах углового сближения-расхождения того и другого – с периодом, равным периоду их обращения. Можно, конечно, продолжать валять дурака и полагать, что Троянцы «колеблются» - в чудовищных по размерам «областях устойчивости» и с чудовищным по длительности периодом. Но такие колебания, по всем теоретическим раскладам, должны быть чудовищно нелинейными. А у нелинейных колебаний, как назло, период зависит от амплитуды. Чего в случае Троянцев не наблюдается! Но почему Троянцы оказываются сосредоточены лишь на двух зафиксированных по отношению к Юпитеру участках его орбиты? Мы рассмотрели такую задачу: частотная воронка Юпитера не достаёт до скоплений Троянцев, и они движутся, тяготея только к центру частотной воронки Солнца – положение которой изменяется из-за её «обращения», в противофазе с обращением Юпитера, около их барицентра. При таких условиях, обращение астероида, долговременно-синхронное с обращением Юпитера, возможно лишь при двух средних углах отстояния астероида от Юпитера, как раз ±60о [Г8] – в согласии с опытом. И это при том, ещё раз отметим, что тяготение Юпитера на Троянец не действует! Более того, подход [Г8] позволяет прояснить сценарий, по которому пополняются скопления Троянцев Юпитера. В эти скопления попадают астероиды из главного пояса, которым удаётся избежать «сметающего» действия частотной воронки Юпитера [Г8]. О каком «сметающем» действии речь? Да взгляните ещё раз на Рис.2.10. Слишком бросается в глаза выраженная резкость внешнего и внутреннего краёв главного пояса астероидов. Официальная наука оставляет без комментариев этот поразительный факт – ибо ей и сказать-то нечего. Мы же этот факт легко объясняем: изнутри пояса, астероиды «подчищаются» частотной воронкой Марса, а снаружи – частотной воронкой Юпитера. Представьте: летел астероид, притягиваясь только к Солнцу, и вдруг он попадает в область планетарного тяготения. Скачком изменяется его локально-абсолютная скорость, бывшая эллиптическая траектория становится гиперболической… Короче, в области планетарного тяготения, такой астероид совершает пролётный «гравитационный манёвр», уводящий его с прежней околосолнечной орбиты. Такие же гравитационные манёвры с некоторых пор лихо закладывают управленцы полётами дальних космических зондов. Только эти управленцы помалкивают про то, что границы областей планетарного тяготения – резко выражены. А мы – ещё раз бросим взгляд на Рис.2.10. Вот же они – свидетельства о границах! Чему учит нас феномен Троянцев? А тому, что точек либрации, предсказываемых законом всемирного тяготения, в реальности-то нету. Нас пытались образумить, приводя пример космического зонда SOHO, который подвесили в точке либрации между Землёй и Солнцем – на полутора миллионах километрах от Земли. Но даже официальная теория гласит, что эта точка либрации неустойчива. И поначалу никто не скрывал, что SOHO удерживали между Землёй и Солнцем, используя подработку двигателем! А тогда, с неменьшим успехом можно было, через подработку двигателем, удерживать зонд около точки между Солнцем и Землёй, отстоящей от Земли не на полтора миллиона километров, а, скажем, на один миллион – эта точка тоже находится за пределами области земного тяготения, радиус которой составляет около 900 тысяч километров. Резюмируем: феномен Троянцев, поначалу считавшийся триумфом закона всемирного тяготения, обернулся грандиозным проколом этого закона. Ибо движение Троянцев не объясняется в рамках представлений о точках либрации – но легко объясняется на основе модели унитарного действия тяготения (2.8)! Спрашивается: если области тяготения планет имеют выраженные границы, то имеет ли такую границу область солнечного тяготения? 2.11. Граница области солнечного тяготения. Ранее мы верили рассказам астрономов о долгопериодических кометах – с периодами обращения, по сильно вытянутым эллиптическим орбитам, вплоть до миллионов лет [С3]. При таких периодах обращения, скорости в афелиях ничтожны, поэтому считается, что большую часть времени такие кометы пребывают в окрестностях своих афелиев – и, соответственно, на интервале удалений 50000-150000 а.е. (астрономическая единица, средний радиус орбиты Земли) существует область повышенной концентрации комет [С3], называемая также облаком Оорта. Если это всё правда, то граница солнечного тяготения должна находиться за пределами облака Оорта. Но на чём основаны рассказы о долгопериодических кометах? Движение комет наблюдается лишь в центральной области Солнечной системы – когда у них имеются выраженные хвосты. Величины же афелиев в 50000-150000 а.е. основаны исключительно на прогнозах, сделанных по результатам анализа наблюдаемых участков траекторий комет. Но прогнозы не обладают доказательной силой. Да и кто наблюдал предсказанное возвращение кометы спустя миллион лет? Достоверные свидетельства имеют совсем другой временной масштаб. Если отбросить курьёзную историю с кометой Гершель-Риголе [Г9], то комета с самым большим удалением в афелии, предсказанные возвращения которой достоверно наблюдались неоднократно – это знаменитая комета Галлея, с периодом обращения около 76 лет. Но её удаление в афелии составляет всего около 35 а.е. [А1]. Имеются ли астрономические свидетельства о том, что солнечное тяготения действует на больших удалениях, чем 35 а.е.? Да, относительно недавно такие свидетельства появились. За орбитой Плутона обнаружили т.н. пояс Койпера. Так астрономы называют группу астероидов, которые обращаются в интервале удалений примерно от 30 до 50 а.е. [ВЕБ13]. Подавляющее большинство объектов пояса Койпера движется по орбитам, близким к круговым, и имеет периоды обращения 260-320 лет [ВЕБ14]. Поразительной особенностью пояса Койпера является то, что его «внешняя граница… на расстоянии 47 а.е. от Солнца выражена очень резко» [ВЕБ13] (на этот факт обратил наше внимание А.Зеберг [З1], который предположил, что по этому краю и проходит граница области солнечного тяготения). Для объяснения этой «резкой выраженности» выдвигали гипотезу о наличии в районе пояса Койпера ещё не обнаруженной планеты, «чьё гравитационное воздействие не позволяет астероидам «разбредаться» [ВЕБ13]. Похоже, нелепость этой гипотезы бросается в глаза не только нам, поскольку резкость внешнего края пояса Койпера уже включают в списки фактов, не имеющих научного объяснения [ВЕБ15]. Что означает резкость внешнего края пояса Койпера? Это означает, что, вплоть до этого края, наблюдается обращение малых тел по почти круговым орбитам – т.е., несомненно, под действием солнечного тяготения – тогда как за пределами этого края такого обращения не наблюдается. Разумеется, «внешняя граница пояса не служит непреодолимым барьером, и 43 астероида (4% от известного их количества) уходят за её пределы… по сильно вытянутым орбитам» [ВЕБ13]. «Самую вытянутую орбиту… имеет 2000 ОО67 с периодом обращения вокруг Солнца 13300 лет» [ВЕБ14]. Опять же, эта цифра имеет чисто прогнозный характер – она получена на основе анализа небольшого участка траектории объекта на удалениях, больших чем 47 а.е. Причём, анализ проводился при допущении о том, что на этих удалениях солнечное тяготение действует. Но если это допущение ошибочно, то прогнозы, сделанные для убегающих койпероидов – совершенно неверны. Если судить по фактам, а не по прогнозам, то круговые орбиты койпероидов доказывают, что они находятся в области солнечного тяготения – но в области, где почему-то не наблюдаются замкнутые орбиты, одни лишь уходящие траектории отнюдь не доказывают наличие там солнечного тяготения. Но ведь на сегодня, за внешний край пояса Койпера вылетели четыре дальних космических зонда: «Пионеры-10,11» и «Вояджеры-1,2»! Полёт каждого из них плотно контролировался средствами дальней космической связи – и, значит, имелись четыре блестящие возможности получить прямой ответ на вопрос о том, является ли внешний край пояса Койпера границей солнечного тяготения! Главный пограничный эффект заключался бы в том, что, пока зонд двигался в области солнечного тяготения, его гелиоцентрическая скорость уменьшалась бы из-за наличия ускорения к Солнцу, а после пересечения им границы это уменьшение гелиоцентрической скорости прекратилось бы. Судя по отсутствию официальных сообщений о таком эффекте, он и не имел места. Однако, именно этот эффект мы выявили при анализе траекторных данных, которые находились в свободном доступе на официальном сайте NASA [ВЕБ16]. Разумеется, точные траекторные данные – это важная научная тайна, поэтому в свободном доступе находились грубые данные. Они были округлены в достаточной, по мнению специалистов из NASA, степени – чтобы их прямое использование не дало ничего, заслуживающего внимания. Тем не менее, мы нашли способ обработки этих данных, на два порядка повышающий точность представления гелиоцентрической дальности зонда [Г9]. По уточнённым данным мы находили уточнённую гелиоцентрическую скорость зонда – её результирующие значения, на интервале дальностей 30-70 а.е., приведены на Рис.2.11 для случая «Вояждера-2» [Г9]. На первый взгляд может показаться, что разбиение изображённого на диаграмме массива точек на две части, с переломом в области 49 а.е., выглядит искусственно. Но заметим, что характер разброса точек принципиально изменяется при переходе через область 49 а.е. А именно: при дальностях до 49 а.е, разброс точек неупорядочен, а далее он приобретает ярко выраженную упорядоченность, в которой отчётливо просматриваются две обособленные последовательности скачков. Так и должно быть, если разброс точек обусловлен, главным образом, грубостью использованных значений гелиоцентрических широт и долгот, и если скорость на дальностях до 49 а.е. уменьшалась, а далее она оставалась постоянной. О таком поведении скорости свидетельствуют и два линейных тренда, построенные для двух участков разбиения массива. Причём, крутизна первого тренда соответствует, на участке 47-49 а.е., величине ускорения 2.8?10-6 м/с2, которая мало отличается от величины ускорения свободного падения к Солнцу на дальности 48 а.е. – 2.6?10-6 м/с2. Такое согласие также свидетельствует о том, что наш анализ данных о траектории «Вояджера-2» не содержит грубых ошибок.
Рис.2.11 Едва ли можно сомневаться в том, что не мы первые обнаружили исчезновение ускорения свободного падения к Солнцу у космических аппаратов, вылетавших за внешний край пояса Койпера. Подобный феномен был бы немедленно выявлен группой слежения за полётом. Но специалисты, работавшие с «Пионерами» и «Вояджерами», не сообщили об этих феноменах, а также о скачках допплеровского сдвига несущей при радиосвязи с аппаратами – на их выходе за внешний край пояса Койпера. А ведь знание величин этих скачков, при известных векторах выхода четырёх аппаратов из Солнечной системы, дало бы возможность определить вектор скорости Солнечной системы в Галактике. Такое определение – более быстрое и точное по сравнению с методами, основанными на наблюдениях вековых движений звёзд – стало бы научной сенсацией. Но, увы, официальная наука в очередной раз умолчала о фактах, которые не уложились в концепцию «всемирного тяготения». Весьма показательна и реакция хозяев использованных нами траекторных данных. Не прошло и двух суток с момента публикации статьи [Г9] и размещения анонсов о ней на форумах в Интернете, как на сайте NASA [ВЕБ16] закрыли свободный доступ к этим траекторным данным, которые до того пылились там лет пятнадцать. Значит, было отчего задёргаться! Но это ещё не всё. Специалисты, рулившие «Пионерами» и «Вояджерами», ранее выдали статью [А2] о необъяснённом аномальном ускорении «Пионеров» к Солнцу – причём, величина этой «аномалии» на четыре порядка меньше, чем скачкообразное обнуление ускорения на границе пояса Койпера, о котором они умолчали. Эту статью [А2] широко разрекламировали. Толпы энтузиастов кинулись наперебой выдвигать самые фантастические гипотезы для объяснения «аномалии «Пионеров». Сильна была их уверенность в том, что они искали объяснения для реального физического эффекта. Но от этой уверенности ничего не остаётся, если внимательно посмотреть на приведённый авторами график (доступный также на [ВЕБ29]). Он иллюстрирует остаточные разности допплеровской скорости (измеряемой минус предсказываемой) для «Пионера-10» на семилетнем интервале. Заметно, что на систематический линейный рост этих остаточных разностей - на основе которого и сделали вывод об «аномальном ускорении» - наложена слабая раскачивающаяся волна с периодом в один год. Едва ли можно серьёзно говорить о том, что космический аппарат, движущийся где-то на периферии Солнечной системы, имеет годичную, да ещё раскачивающуюся, модуляцию своей скорости. Между тем, известно, что при машинной обработке потоков данных, имеющих периодические составляющие, появление такого рода «раскачек» при определённых параметрах фильтрации – обычное дело. Едва ли можно сомневаться в том, что названная годичная волна на графике не соответствует реальному физическому эффекту, а является «эффектом обработки». И если фильтрация при обработке данных допускает «пролезание» периодической паразитной компоненты, то «пролезание» линейной паразитной компоненты она должна допускать тем более. Было бы странно, если линейная паразитная компонента при этом отсутствовала бы! Добавим, что мы усматриваем важное косвенное свидетельство о том, что заявленное «аномальное ускорение аппаратов к Солнцу» является не реальным физическим эффектом, а «эффектом обработки». Речь о том, что для аппаратов разных конструкций (Пионер-10 и -11, Галилео, Улисс) «аномальное ускорение» оказалось практически одинаковым в огромном диапазоне расстояний от Солнца - от 1.3 до 67 а.е. [А2]! Самым простым объяснением такого чуда является допущение об одинаковом паразитном эффекте, имевшем место при обработке различных сегментов данных – одной и той же программой [А2]. И неспроста авторы [А2], которые могли представить график на 20-летнем интервале, ограничились семилетним интервалом. Одним годом больше – и раскачивающаяся годичная волна уже бросалась бы в глаза всем. Создаётся стойкое впечатление, что главной целью публикации [А2] было внушение научному сообществу ложной уверенности в том, что, с точностью до ~10-8 см/с2, солнечное тяготение действует в полном согласии с законом всемирного тяготения – на дальностях вплоть до 60 а.е. и более. Чтобы никто даже не заподозрил, что область солнечного тяготения имеет чёткую границу! 2.12. Малость радиуса действия тяготения Луны. Согласно закону всемирного тяготения, тяготение Луны действует вплоть до границ Вселенной. Но самыми значимыми его проявлениями считаются, во-первых, динамическая реакция Земли на Луну, т.е. обращение Земли, в противофазе с обращением Луны, около их общего центра масс, и, во-вторых, лунные приливы в океанах. Однако, правда заключается в том, что тяготение Луны действует лишь в небольшой окололунной области, примерно до 10000 км от лунной поверхности – и, таким образом, оно даже до Земли далеко не достаёт. Поэтому пара Земля-Луна движется весьма своеобразно (2.14), ведь земное тяготение на Луну действует, а лунное тяготение на Землю – нет (2.13). И океанские приливы порождаются отнюдь не тяготением Луны (2.15). Интересно, что тяготение Луны организовано не по принципу планетарного тяготения. Если Луна имела бы собственную частотную воронку, то, при радиолокации Луны узкополосным сигналом, отсутствовал бы вклад в эффект Допплера (1.9), соответствующий изменению геоцентрического расстояния до Луны из-за того, что её орбита не является круговой. В действительности же этот вклад имеет место [Б2]. Кстати, опять же: аномально организованное тяготение Луны порождается отнюдь не её веществом. Дело в том, что имеются убийственные свидетельства о том, что Луна представляет собой не сплошное тело, а тонкостенную оболочку – например, по результатам работы сейсмодатчиков на поверхности Луны. Сейсмические события, на которые реагировали эти сейсмодатчики, вызывали и искусственно, для чего на Луну направляли отработанные разгонные ступени ракет. Поразительным было то, что «лунотрясения» длились невероятно долго. Так, после удара о поверхность Луны третьей ступени ракеты Сатурн, использованной для разгона корабля Аполлон-13, «звон» «детектировался в течение более четырёх часов. На Земле, при ударе ракеты на эквивалентном удалении, сигнал длился бы всего несколько минут» [Л6] (перевод наш). Сейсмические колебания с такой высокой добротностью нетипичны для сплошного тела, и, наоборот, они характерны для полого резонатора. Гипотеза об организации аномального тяготения Луны изложена в [Г14]. Здесь мы имеем исключительный случай, когда тяготение меньшего по рангу тела действует совместно с тяготением большего по рангу тела – но тяготение меньшего тела на некотором радиусе полностью сходит на нет. Малость этого радиуса проявилась в первых же полётах космических аппаратов в окололунном пространстве. Об этом свидетельствует анализ, во-первых, пролётных окололунных траекторий, и, во-вторых, орбит искусственных спутников Луны – эти орбиты возможны лишь в той области, где лунное тяготение доминирует над земным. Согласно закону всемирного тяготения, такой областью считается т.н. сфера действия Луны, радиус которой составляет 66000 км [Л4]. Но практика окололунных полётов указывает на то, что фактический радиус области лунного тяготения имеет значительно меньшую величину. Так, советский аппарат «Луна-1», запущенный 2 января 1959 г., впервые в истории космонавтики достиг окрестностей Луны. Планировалось попадание в Луну, которое должна была обеспечить правильность вектора скорости аппарата в конце разгона. Но «из-за ошибки по углу места в 2о… допущенной при работе наземных радиотехнических средств пеленгации и управления ракетой, двигатель… выключился позже назначенного момента, что и послужило причиной промаха» [ВЕБ17]. Аппарат прошёл на расстоянии около 6000 км от поверхности Луны [Ч1] и, поскольку при разгоне ему была сообщена гиперболическая скорость, вышел за пределы сферы действия Земли, «превратившись… в первую искусственную планету Солнечной системы» [Ч1]. Даже тех скудных данных о параметрах полёта «Луны-1», которые имеются в свободном доступе, достаточно для того, чтобы рассчитать угол поворота траектории аппарата из-за действия лунного тяготения. Расчёт, основанный на концепции сферы действия Луны (с радиусом 66000 км), даёт для угла поворота траектории величину около 11о [Г10]. Радиосигналы «Луны-1» принимались в течение ещё суток с небольшим после того, как она разминулась с Луной [Л5], и обнаружение поворота траектории на 11о не представляло особых сложностей. Но, странным образом, об этом повороте ничего не говорится даже в книге [Л5], где полёт «Луны-1» описан весьма подробно. Поскольку официальные источники молчат, обратимся к источникам неофициальным. Баллистики, обсчитывавшие первые полёты к Луне, недоумевали: выходило, что поворот оказался значительно меньше того, который был бы по ньютоновской теории. «Заказчик ставил задачи со «странными» исходными данными, по расчёту управления лунным спутником; на вопрос «откуда такие цифры?» - был ответ «не ваше дело» [У1]. Между тем, малость поворота траектории «Луны-1» могла быть обусловлена малостью радиуса области лунного тяготения, т.е., прохождением аппарата лишь по небольшому участку на её периферии. Далее, аппарат «Луна-3», запущенный 4 октября 1959 г., впервые произвёл пассивный облёт Луны. Траектория облёта состояла из гиперболического участка в области тяготения Луны и последующего эллиптического разворота, обусловленного тяготением Земли. Из траекторных данных, имеющихся в свободном доступе [Л5], прямо следует малость области тяготения Луны: наша оценка для высоты его границы над лунной поверхностью составила 10000 км [Г10]. Теперь спрашивается: известны ли случаи, когда искусственный спутник Луны имел орбиту с апоселением (наиболее удалённой точкой от Луны) выше, чем 10000 км от поверхности? В 60-е – 70-е годы ХХ века, максимальную высоту апоселения имел «Лунар Орбитер-5»: 6050 км [К5]. Впоследствии эта цифра была увеличена: американский зонд Clementine (1994) имел высоту апоселения 8300 км, американский зонд Lunar Prospector (1998) – 8500 км [ВЕБ18], а китайский «Чан Э» (2007) – 8600 км [ВЕБ19]. Что касается зонда Kaguya (2007), то для высоты его первого, самого высокого, апоселения Японское космическое агентство назвало цифру 11741 км [ВЕБ20], и её повторили многие информационные агентства. Но эта цифра может быть несколько завышена, поскольку она явилась результатом прогноза, сделанного сразу же после главного тормозного манёвра [ВЕБ20]. Во всяком случае, все названные цифры значительно меньше, чем радиус сферы действия Луны. Поразительно то, что отечественные и американские специалисты, ещё полвека назад запускавшие первые аппараты к Луне, отлично знают про малость области её тяготения. Но эта информация до сих пор представляет собой важную научную тайну, поэтому современные японские, китайские и европейские аппараты, отправляемые к Луне, нарываются на гравитационные сюрпризы. Нам известно про два проекта, в которых производились попытки захвата аппарата тяготением Луны на удалениях, значительно больших 10000 км. В обоих случаях официально сообщалось, что захват произошёл – но новоиспечённый спутник Луны оказывался не в состоянии выполнять запланированную научную программу. Первый из этих двух проектов – полёт японского зонда MUSES-A (Hiten), запущенного в 1990 г. «Во время… первого пролёта Луны предстояло выполнить две задачи: использовать гравитационное поле Луны для увеличения скорости КА и для повышения апогея орбиты, а также отделить от основного КА малый субспутник «Хагоромо», которому предстояло стать искусственным спутником Луны… Отделение «Хагоромо» от базового блока произошло в соответствии с программой полёта в тот момент, когда «Хитен» пролетал на высоте 20 тыс. км от поверхности Луны. Однако собственный передатчик «Хагоромо» вышел из строя, и в центре управления на Земле не удалось получить никаких данных с аппарата и подтвердить его выход на окололунную орбиту. Позже, используя большой оптический телескоп, японским астрономам удалось увидеть, как «Хагоромо» движется по орбите Луны… но как научный аппарат «Хагоромо» был потерян» [ВЕБ21]. Эта официальная версия о выходе «Хагоромо» на окололунную орбиту выглядит неубедительно, поскольку в ней умалчивается о том, удался ли запланированный гравитационный манёвр основного модуля. Более того, в дальнейшем Hiten совершил, как сообщалось, ещё несколько гравитационных манёвров на пролётах вблизи Луны – но, опять же, японцы умалчивали о подробностях. Похоже, хвалиться-то было нечем. Зато известно, что на одиннадцатом пролёте, когда аппарат был переведён на окололунную орбиту, он проходил на расстоянии всего 423 км от поверхности Луны [ВЕБ21]! Второй же из этих проектов – полёт зонда SMART-1 Европейского космического агентства (ЕКА, ESA). Зонд был выведен ракетой-носителем на околоземную стартовую орбиту в сентябре 2003 г. Затем зонд в течение года с небольшим "раскачивал" орбиту с помощью плазменного двигателя малой тяги, подтягивая апогей к орбите Луны. Планировался захват зонда тяготением Луны при первом же входе в т.н. сферу действия Луны, на удалении от неё около 60000 км. Затем, после снижения на окололунную орбиту, планировалось сделать множество фотографий лунной поверхности. В частности, обещали заснять следы пребывания американских астронавтов на Луне - поэтому миссия была широко прорекламирована. Специалисты хорошо знали цену этим обещаниям - известно, что Луна чуть не постоянно "скрипит" из-за слабых "лунотрясений", что там имеет место электростатическое "оползание" грунта, и что движение линии терминатора (границы день-ночь) по поверхности Луны сопровождается пыльной бурей. В течение месяца полоса пыльной бури дважды прокатывается по поверхности Луны, и наивно полагать, что от "следов астронавтов" что-то могло сохраниться. Специалисты знали об этом, но помалкивали – как и о том, что лунное тяготение действует на космические аппараты не далее 10000 км от поверхности Луны. Поэтому в ESA не подозревали, что SMART-1 далеко не долетит до области тяготения Луны, и что этот проект обречён на провал. Теоретически, зонд следовало ввести хотя бы в ближайшую к Земле область сферы действия Луны – с селеноцентрической скоростью, меньшей чем местная круговая – и зонд захватился бы тяготением Луны. Но сразу после того как такой ввод был произведён, что-то пошло «не так». На официальном сайте ESA перестали появляться обновления, оперативно освещавшие полёт SMART-1. После неприлично затянувшейся паузы, ESA задним числом сообщило о том, что зонд был захвачен тяготением Луны, затем, на малой тяге, переведён на низкую полярную орбиту, и даже передал на Землю несколько фотографий участков лунной поверхности. После очередной паузы, эти фотографии были опубликованы. Приглядевшись, специалисты узнали в них снимки тридцатилетней давности, сделанные другими космическими аппаратами. После ещё нескольких месяцев молчания о том, чем занимается SMART-1 в окололунном пространстве, ESA заявило о том, что зонд выполнил свою миссию и будет разбит о поверхность Луны. «SMART-1 спрятал концы в лунную пыль» - издевались информационные агентства. Даже неспециалисты подозревали, что ESA дурачило общественность! О том, как это всё происходило в реальном времени, красноречиво свидетельствует весёлая дискуссия на форуме портала "Новости космонавтики" [ВЕБ22]; доступен также конспект этой дискуссии [ВЕБ23]. Кстати, вывод о лжи ESA можно было сделать сразу после того, как были опубликованы данные [ВЕБ24], описывающие «захват» зонда тяготением Луны. Этих данных достаточно для реконструкции, во-первых, полуэллипса подлёта, по которому зонд двигался в поле тяготения Земли перед тем как, вблизи апогея, войти в сферу действия Луны, и, во-вторых, первого полуэллипса снижения в сфере действия Луны. Даже старшеклассник мог бы убедиться в том, что эти два полуэллипса не «сшиваются» друг с другом [Г10] – а, значит, официальная информация о захвате зонда тяготением Луны и о его дальнейшей судьбе является фальсификацией. Что же в действительности произошло с зондом SMART-1? По-видимому, при малости области тяготения Луны, зонд просто не вошёл в эту область – и, как ни в чём не бывало, продолжил свой полёт по эллиптической орбите вокруг Земли. Самое разумное, что могли сделать руководители полёта в такой ситуации – это проверить, не «захватится» ли зонд на следующем пролёте через сферу действия Луны. До срока завершения миссии можно было сделать ещё несколько попыток такой проверки [Г10]. Но чуда не произошло. Чтобы зонд добрался до области лунного тяготения и в самом деле захватился, требовалось ещё поднять апогей и значительно увеличить апогейную скорость. Увы – на малой тяге и с почти израсходованными запасами рабочего вещества – выполнение этой задачи было совершенно нереально. По всей вероятности, зонд до сих пор летает по эллиптической орбите, которая почти дотягивается до орбиты Луны. А всё потому, что, на расстоянии уже в несколько десятков тысяч километров от Луны, её тяготение, вопреки официальным воззрениям, не действует. 2.13. Луна не притягивает Землю! Если область тяготения Луны далеко не достаёт до Земли, то кинематика пары Земля-Луна должна отличаться от той, что предсказывает закон всемирного тяготения. Так ли это? Рассмотрение обращения Луны вокруг Земли, наряду с орбитальными движениями планет, сыграло важную роль в работе Ньютона над законом всемирного тяготения. Среднее удаление Луны от Земли соответствует среднему периоду обращения Луны как раз в согласии с этим законом. И Лаплас в своей «Системе мира» [Л2] заявил, что полное согласие движения Луны с законом всемирного тяготения является неоспоримой научной истиной. Но! Неспроста же говорят, что достаточно иметь отрывной календарь, чтобы убедиться в том, что Луна летает «неправильно». Согласно закону всемирного тяготения, орбита невозмущённого движения спутника планеты является кеплеровой – эллиптической. Возмущения же, например, из-за действия третьего тела, должны приводить к эволюциям параметров орбиты. Причём, эти параметры должны эволюционировать согласованно: так, приращению большой полуоси должно соответствовать приращение периода обращения в согласии с третьим законом Кеплера. Однако, движение Луны вокруг Земли является вопиющим исключением из этого правила. Достоверно известно – и отражается в Астрономических ежегодниках, см., например, [Г12] – что большая полуось орбиты Луны изменяется, с периодом 7 синодических месяцев, на ~5500 км. Размах соответствующего изменения периода обращения, согласно третьему закону Кеплера, должен составлять ~14 часов. В действительности же, вариация длительности синодического месяца составляет около 5 часов, причём период этой вариации равен не 7 синодическим месяцам, а 14. Таким образом, в случае Луны большая полуось и период обращения эволюционируют несогласованно – как по амплитуде, так и по периодичности. Несомненно, об этой проблеме знали уже первые теоретики движения Луны – в частности, тот же Лаплас. Несомненно, они понимали: никакие «возмущения орбиты» не помогут решить эту проблему, ибо, согласно закону всемирного тяготения, не бывает возмущений, которые приводили бы к тому, что линейные размеры орбиты и период обращения по ней изменяются так несогласованно. Выяснить, почему Луна движется таким странным, с точки зрения закона всемирного тяготения, образом – означало бы вынести приговор этому закону. Поэтому теорию движения Луны строили весьма своеобразно: «теоретики отказались от представления… элементов орбиты Луны в виде рядов… и предпочитают разлагать в ряд сами координаты» [К6]. Такой подход, на наш взгляд, и привёл к тому, что задача о движении Луны превратилась в «одну из самых трудных проблем небесной механики» [К6]. Об ущербности этого подхода косвенно свидетельствует даже тот факт, что получаемые ряды «очень медленно сходятся» [К6], так что в современных теориях число членов этих рядов «измеряется уже тысячами» [ВЕБ25]. Первые их сотни приведены, например, в справочном руководстве [Д2]. Вспомним, что, по логике унитарного действия тяготения, области действия тяготения больших космических тел не накладываются друг на друга. Но случай с Луной является исключением: Луна имеет аномально организованное тяготение, которое, в области своего действия, суммируется с тяготением Земли. Однако до Земли это аномальное тяготение не достаёт (2.12). И тогда мы имеем следующую ситуацию: солнечное тяготение на Луну-болванку не действует, а сообщает ускорение только частотной воронке Земли, по склонам которой движется Луна-болванка – не вызывающая у частотной воронки Земли динамической реакции, т.е. обращения, в противофазе с обращением Луны, около их общего «центра масс». Факт НЕ-обращения Земли около общего с Луной центра масс – наиболее убийственен для закона всемирного тяготения. Мало того, что этот факт весьма нагляден и совершенно однозначен – он ещё и легко проверяем из-за огромной величины соответствующего эффекта. Ведь если названное обращение Земли имело бы место, то центр масс Земли выписывал бы, с периодом в синодический месяц, кривую со средним радиусом около 4670 км! Как официальной науке удаётся до сих пор дурачить общественность насчёт этого «лошадиного» по величине эффекта, которого в действительности не существует? Право, следует признать: эта позорная задача не из лёгких, тут требуются весьма изысканные ухищрения. Для начала нам подсовывают т.н. лунное неравенство, т.е. периодическую компоненту в видимой долготе Солнца, с амплитудой около 6?.4 и периодом в синодический месяц [С3]. Этот феномен интерпретируют как колебания гелиоцентрической долготы Земли, наложенные на годичный дрейф этой долготы. Говорят, что это и есть чёткое свидетельство об обращении Земли около общего с Луной центра масс – мол, и фаза у этих колебаний та, что надо, и амплитуда в точности соответствует значению массы Луны. Ну, неужели! Ещё бы здесь не было точного соответствия – ведь массу Луны рассчитали именно по величине лунного неравенства! Но, заметим: это лунное неравенство, т.е. болтанка гелиоцентрической долготы Земли, свидетельствует не об обращении Земли, а лишь о её одномерных колебаниях – вперёд-назад вдоль текущего участка орбиты. А при полноценном двумерном обращении Земли, имели бы место ещё и аналогичные её колебания поперёк текущего участка орбиты – «от Солнца – к Солнцу». Эти колебания имели бы следующие параметры: период – синодический месяц, амплитуда смещения – 4670 км, амплитуда скорости – 12.3 м/с. Они могли быть легко обнаружены с помощью ряда экспериментальных методик. Но, посмотрим, как здесь обстоят дела в действительности. Наблюдение спектральных линий Солнца. Колебания Земли «от Солнца – к Солнцу» приводили бы, согласно традиционным представлениям, к соответствующим допплеровским смещениям спектральных линий Солнца, с относительной амплитудой ~4.1?10-8. Нам не удалось найти сообщений на эту тему. С учётом того, что спектральные исследования Солнца проводились довольно интенсивно, можно заключить, что этот эффект отсутствует. Такой «нулевой результат» особенно поразителен в контрасте с бурно развивающимся направлением в астрономии – обнаружением планет у далёких звёзд по периодическим изменениям лучевой скорости звезды, вызываемым, как полагают, динамической реакцией звезды на планету. Со статьями по этой тематике можно познакомиться по адресу [ВЕБ26]. Сообщается, что «в 2004 г., используя новые спектрографы, удалось повысить точность измерения лучевых скоростей до 1 м/с» [ВЕБ27]. Вот бы применить эти новые спектрографы, чтобы обнаружить допплеровские смещения спектральных линий Солнца из-за синодических колебаний Земли! Но нет: отчего-то мощь допплеровского метода приводит к сенсациям в случае далёких звёзд, но не срабатывает в случае Солнца, у которого достоверно известны лучевая скорость и многие другие параметры. Приём импульсов пульсаров. Колебания Земли «от Солнца – к Солнцу» приводили бы к систематически накапливающимся запаздываниям моментов прихода импульсов пульсаров (по аналогии с классическим методом Рёмера). Размах этого эффекта, от новолуния до полнолуния, для пульсаров на примерно той же гелиоцентрической долготе и широте, что и Земля за эти полмесяца, составил бы около 0.03 с. Этот эффект вполне заметен, если моменты прихода импульсов редуцировать к центру Земли. Вместо этого, в хронометрировании пульсаров принято редуцировать моменты прихода импульсов к барицентру Солнечной системы [С5,М3]. Но, при такой редукции, относительная величина синодического эффекта составляет 2?4670 км/1 а.е. =6.2?10-5. Эквивалентное изменение периода повторения импульсов, при типичном значении этого периода в 1с, составляет ~60 мкс, тогда как «неопределённость моментов прихода радиоимпульсов на телескоп обычно составляет около 100 мкс» [М3]. При таком положении дел, синодические колебания Земли никак не отразятся на результирующей временной зависимости периода повторения импульсов, сглаженной низкочастотной фильтрацией по методу наименьших квадратов [М3]. Таким образом, информацию о синодических колебаниях Земли полностью теряют – и делают это сознательно! Спрашивается – а почему? Похоже, потому, что отлично знают: если всё делать честно, то никаких синодических колебаний Земли «от Солнца – к Солнцу» не обнаруживается. Радиолокация планет. В рамках традиционного подхода можно было ожидать, что колебания Земли «от Солнца – к Солнцу» проявятся при радиолокации планет двояко: во-первых, через соответствующую периодическую компоненту в допплеровском сдвиге несущей эхо-сигнала, и, во-вторых, через соответствующую периодическую компоненту в задержках на прохождение радиосигнала к планете и обратно. Но не тут-то было. Откуда взяться допплеровским сдвигам из-за приближения или удаления планеты-цели, если локально абсолютные скорости планет равны нулю (1.8)? Как уже отмечалось (1.9), отсутствие допплеровского сдвига при радиолокации удалалявшейся Венеры было достоверно обнаружено Котельниковым с сотрудниками в 1961 г. Одного этого факта было достаточно для того, чтобы повергнуть в прах специальную теорию относительности. Поэтому секрет успешной радиолокации Венеры не афишировался; а экспериментаторы прибегли к другим схемам детектирования эхо-сигнала – в которых ужасная правда про отсутствие эффекта Допплера не слишком бросалась в глаза. Укажем, например, на попытки радиолокации Венеры с применением синхронного детектирования [П3], и даже прямого счёта частоты эхо-сигналов [М4]. В обеих этих методиках узкая полоса, в которую ожидалось попадание частоты эхо-сигнала, предустанавливалась – разумеется, на основе принятых теорий. Но получение откликов здесь не подтверждало принятые теории – оно вообще ничего не подтверждало, поскольку отклики из-за полезных сигналов были неотличимы от откликов из-за шумов [Г11]. Вот в методике Котельникова доказательная сила была: детектирование полезного сигнала было неоспоримо, поскольку чётко различались случаи «сигнал плюс шумы» и «только шумы». А авторы [П3,М4] то ли по забывчивости, то ли намеренно умолчали о главной контрольной проверке, позволявшей уверенно заявлять о том, что они действительно ловили отражённые сигналы. Махнём же рукой на эти забавы экспериментаторов и обратимся к методике измерения пролётных времён радиоимпульсов. Уж тут-то периодические компоненты в расстояниях между Землёй и планетами, из-за синодической болтанки Земли «от Солнца – к Солнцу» должны были проявиться во всём великолепии! Вот даже Шапиро с соавторами соловьём заливается [А3]: «Отношение масс Земля-Луна хорошо определяется из-за того, что при измерениях пролётных времён радиоимпульсов проявляется обращение Земли вокруг центра масс Земля-Луна» (перевод наш). Вы, дорогой читатель, небось подумали, что имеется ряд публикаций, где представлены, по результатам радиолокации, синодические волны у расстояний между Землёй и планетами? Нет, таких публикаций мы не отыскали. Понимаете ли, в чём дело: не обнаруживаются эти синодические волны. А о чём же соловьём заливался Шапиро? Так он и не говорил, что эти волны напрямую обнаруживаются. Их через задницу «обнаруживали» - методом оптимизации многих параметров [А3]. Т.е. изначально принимали, что синодическая болтанка Земли поперёк орбиты существует – и, исходя из этого постулата, обрабатывали массивы данных, чтобы наилучшим образом подогнать под этот постулат значения набора параметров, от которых зависели пролётные времена. В этом и прелесть метода оптимизации многих параметров – что захочешь «доказать», то и «докажешь»! Даже если величина несуществующего эффекта, наличие которого ты «доказываешь», на несколько порядков превышает погрешности измерений! Слежение за автоматическими межпланетными станциями. Осуществлялся плотный радиоконтроль за движением автоматических межпланетных станций. По допплеровским измерениям при связи со станцией можно судить о её геоцентрической лучевой скорости, а интегрирование временной зависимости скорости дало бы временную зависимость дальности – в дополнение к измерениям пролётных времён радиоимпульсов. Полёт к Венере обычно длится около 3.5 месяцев, и можно было ожидать, что на результирующих зависимостях скорости и дальности обнаружатся синодические волны из-за болтанки Земли поперёк своей орбиты. «Покажите же нам эти волны!» - просим мы. Вот статья [А4], авторы которой, якобы, уточняли массы Земли и Луны по результатам слежения за АМС «Венера-4» - «Венера-7». Авторы не привели ни одной (!) экспериментальной цифры, характеризующей скорость и удаление станций. А занимались они решением задач оптимизации многих параметров (да-да, здесь напрямую тоже не получается). В число согласуемых параметров, наряду с координатами места импульсной коррекции полёта и векторами скорости станции до и после коррекции, входили величины гравитационных параметров Земли и Луны. Беря отношение этих двух гравитационных параметров, получали искомое отношение масс. Ужас какой-то! Зачем же было выворачиваться, чтобы с такими трудами получить неоднозначный результат? Ведь зависимости скорости и дальности у АМС «Венера-4» - «Венера-7» дали бы однозначный результат напрямую! Что же такое секретное обнаружилось в этих зависимостях?! Не кажется ли вам, дорогой читатель, что, в вопросе о синодической болтанке Земли поперёк орбиты, разные авторы занимаются, в сущности, одним и тем же? Но вот статья [А5] – похоже, это исключение из правила! Её авторы использовали результаты слежения за АМС «Маринер-6» и «Маринер-7». На этот раз речь идёт именно о «синусоиде в дальномерных и допплеровских данных», по амплитуде которой отношение масс Земля-Луна «определяется прямо и надёжно». Примечательно, что середины трёхмесячных интервалов, данные которых были взяты в обработку, отстояли примерно на четыре месяца от стартов аппаратов – когда эти аппараты, подбираясь к орбите Марса, имели примерно те же текущие гелиоцентрические долготы, что и Земля. При этом «синусоида в дальномерных и допплеровских данных» однозначно свидетельствовала бы о колебаниях Земли «от Солнца – к Солнцу». Но ведь не бывает такого, чтобы у всех по-честному не получалось – а тут вдруг получилось. И точно: секрет в том, что же эти авторы понимали под той самой синусоидой. Оказывается, за искомое отношение масс Земля-Луна они принимали такое, «при котором устранялся, по методу наименьших квадратов, месячный цикл остаточных уклонений в данных слежения» (перевод наш). Выходит, что «месячный цикл» наблюдался в… остаточных уклонениях? Но по отношению к чему могли получаться эти остаточные уклонения, если не по отношению к теории? – в которой считалось, что Земля обращается вокруг «центра масс» Земля-Луна! Значит, если Земля двигалась бы в согласии с теорией, то никаких «остаточных уклонений, с циклом в месяц» не наблюдалось бы. Но если, вместо принятого в теории обращения, Земля совершает колебания с такой же амплитудой – вдоль текущего участка орбиты – то главная часть остаточных уклонений имела бы ту же самую амплитуду и месячную цикличность. Это именно то, о чём говорят авторы! Как ни старались они выдать чёрно-белое за бело-чёрное, а, фактически, они доказали: синодической болтанки поперёк орбиты у Земли нет. Статистика землетрясений. Если исходить из того, что вероятность землетрясений повышается при максимальных возмущениях локальных векторов силы тяжести, то даже по статистике землетрясений можно в некоторой степени судить о характере движения Земли в кинематике пары Земля-Луна. Согласно традиционному подходу, число землетрясений должно увеличиваться вблизи сизигий, т.е. новолуний и полнолуний. Согласно же нашему подходу, Луна не вызывает силовых реакций на Земле, поэтому число землетрясений должно увеличиваться, когда максимальны ускорения Земли, обусловленные её колебаниями вдоль текущего участка орбиты – а эти ускорения максимальны не в сизигиях, а, наоборот, в квадратурах – когда угол между векторами «Земля-Солнце» и «Земля-Луна» составляет 90о. На Рис.2.13 представлена статистика числа землетрясений по всему земному шару за сейсмически весьма активный 2003 год; использованы общедоступные данные официального сайта Всемирного центра по изучению землетрясений [ВЕБ28]. Одна точка обозначает число землетрясений с магнитудой 1.0-4.0 на интервале в трое суток. Треугольниками обозначены моменты квадратур.
Рис.2.13 Здесь мы усматриваем: число минимумов, приходящихся на квадратуру – 3; число максимумов, приходящихся на сизигию – 6; а число максимумов, приходящихся на квадратуру – 17. Таким образом, даже поверхностный субъективный анализ показывает, что количество соответствий, подтверждающих увеличение числа землетрясений вблизи квадратур, почти вдвое превышает количество соответствий, не подтверждающих это. Т.е., приведённая статистика землетрясений свидетельствует в пользу одномерных синодических колебаний Земли вдоль текущего участка орбиты [Г11]! 2.14. Ох, уж эти странности в движении Луны! Особенности движения Луны по небосводу издавна представляли большой практический интерес. Чем лучше знаешь движение Луны, тем точнее можешь решать навигационные задачи. Поэтому отклонения от равномерного движения Луны хорошо известны, они даже имеют специальное название: неравенства в движении Луны. Самое значительное из этих неравенств – т.н. большое эллиптическое. Оно отражает факт эллиптичности орбиты Луны, из-за чего апогейная скорость движения Луны меньше, чем перигейная. Если, как обсуждалось выше (2.13), кинематика пары Земля-Луна такова, что Луна выписывает, около условного центра, двумерную кривую, а Земля совершает около этого центра одномерные колебания вдоль текущего участка своей орбиты, то это с полной очевидностью проявлялось бы через соответствующее неравенство в движении Луны. Вот вы, дорогой читатель, как полагаете – проявляется оно или нет? Конечно, проявляется – да притом с полной очевидностью. Это неравенство – т.н. вариация. Именно вариация и соответствующие ей периодические изменения геоцентрического расстояния до Луны отражают – практически, в чистом виде – факт двумерного полёта Луны и одномерных колебаний Земли [Г12]. Именно такие, как у вариации, положения нулей и максимумов, для поправки в видимую долготу Луны, должны иметь место, если двумерное движение Луны и одномерные колебания Земли сфазированы следующим образом: в моменты квадратур Земля находится на максимальном удалении от центра колебаний, причём в сторону, противоположную Луне, а в моменты сизигий (новолуний и полнолуний) Земля проходит через центр колебаний. Таким образом, одномерность колебаний Земли в кинематике пары Земля-Луна имеет самое прямое подтверждение – астрооптическое. По-простому, это называется «подтверждение методом пристального вглядывания». Но это ещё не всё. В отличие от вариации, положения нулей и максимумов которой фиксированы по отношению к линии Земля-Солнце, у ещё одного главного неравенства в движении Луны, т.н. эвекции, положения нулей и максимумов являются плавающими. Это неравенство также находит простое объяснение на основе наших исходных допущений о том, что солнечное тяготение, будучи «отключено» в области земного тяготения, на Луну не действует, а Луна летает в области земного тяготения как болванка, которая не действует на Землю. Ясно, что синодические колебания Земли и её частотной воронки, вперёд-назад вдоль текущего участка околосолнечной орбиты, порождаются не воздействиями Луны и не воздействиями Солнца. Нам придётся допустить, что эти колебания были специально организованы – чисто программными манипуляциями. Для этого в алгоритм, управляющий орбитальным движением земной частотной воронки (2.8), внесли соответствующую модификацию. Зачем это понадобилось? В результате этой процедуры земная частотная воронка не находится в чистом орбитальном «свободном падении», а испытывает периодические ускорения-замедления своего орбитального полёта, так что Луна-болванка движется по склонам этой «болтающейся» частотной воронки. Из равенства синодическому месяцу периода этой «болтанки» напрашивается вывод: принудительные колебания земной частотной воронки понадобились для того, чтобы быть синхронизатором орбитального движения Луны, играя роль параметрического задатчика периода её обращения [Г12]. Что это означает? Ускорения земной частотной воронки вперёд-назад, обусловленные её одномерными колебаниями, должны порождать противоположные «ускорения сноса» Луны-болванки. Физический смысл здесь прост и нагляден: если тело свободно движется в «инерциальном пространстве», которое само имеет ускорение, то это тело движется по отношению к «инерциальному пространству» так, как будто это тело имеет противоположное ускорение. И вот эти «ускорения сноса» являются слабыми воздействиями, возмущающими движение Луны. Из-за строгой периодичности этих возмущающих воздействий происходит синхронизация орбитального движения Луны: её движение подстраивается так, чтобы период обращения – между двумя новолуниями – был равен периоду синхронизирующих воздействий. Но, при постоянстве этого периода, переменные «ускорения сноса» должны приводить к переменным эволюциям параметров орбиты Луны: апогейного и перигейного расстояний, а также эксцентриситета. Выражения, описывающие эволюции этих параметров эллиптической орбиты при малых возмущающих воздействиях, приведены, например, в [А6]. Мы выполнили машинное интегрирование этих выражений для орбитального движения Луны, возмущаемого вышеназванными «ускорениями сноса». Полученные предсказания для эволюции параметров орбиты, практически, совпадают с фактическими изменениями этих параметров – и по фазе, и по амплитуде [Г12]. Таким образом, главные «странности» движения Луны вполне адекватно объясняются на основе наших представлений. На это нам скажут, что эти «странности» адекватно объясняются и на основе ньютоновских представлений. Да где же она там, адекватность? Ньютон объяснял и вариацию, и эвекцию одним и тем же механизмом – возмущениями движения Луны со стороны Солнца. При этом он помалкивал о том, что не бывает возмущений, при которых период обращения и большая полуось эволюционируют несогласованно (2.13). Хуже того: если и вариация, и эвекция являлись бы результатами возмущений со стороны Солнца, то одна часть возмущающего воздействия шла бы на вариацию, а другая – на эвекцию. Увеличение амплитуды одной из них происходило бы за счёт уменьшения амплитуды другой. В действительности же, эти два главных неравенства в движении Луны проявляются совершенно независимо друг от друга, и их амплитуды постоянны. Значит, их причины – разные. Об этом мы и говорим: вариация – это чисто геометрический эффект, обусловленный одномерностью колебаний Земли при двумерном движении Луны, а эвекция – это динамический эффект, обусловленный «ускорениями сноса» Луны из-за тех самых одномерных колебаний земной частотной воронки. Не нужно быть особо одарённым, чтобы понять: наши объяснения главных «странностей» в движении Луны – поадекватнее, чем ньютоновские. Уместно добавить, что все вышеперечисленные выводы насчёт пары Земля-Луна выносились на открытое обсуждение на астрономических форумах Интернета, и тамошние специалисты публично обещали размазать автора по стеночке. Но трудно переть против очевидных фактов, поэтому дальнейшей реакцией специалистов было либо гробовое молчание, либо злобное шипение. Впрочем, бывали и другие отклики. Сотрудник одного из НИИ, связанного с космонавтикой, прислал письмо по электронной почте. Он давно слышал про какие-то странности в движении Луны и занялся, в частном порядке, астрономическими наблюдениями за ней. «Я думал, что схожу с ума, - писал он. – Как может Луна так двигаться, если верен закон всемирного тяготения? И вот я натыкаюсь на Ваши статьи про движение Луны. Вы вернули меня к жизни!» Это мы к чему? Ой, как тяжело тем учёным, которые знают правду про движение Луны, но твердят, что она движется «в полном согласии с законом всемирного тяготения»! Какую же устойчивую психику надо иметь – чтобы, при таких делах, не свихнуться?! 2.15. Правда про приливы в океанах. Согласно традиционным воззрениям, лунно-солнечные приливы в океанах происходят из-за глобальных возмущений силы тяжести, обусловленных наложением лунного и солнечного тяготений на земное тяготение и результирующим совместным их действием на вещество Земли – в частности, на океанскую воду. Но выше мы изложили факты, которые отметают эти традиционные воззрения. Во-первых, в области тяготения Земли, солнечное тяготение «отключено». Во-вторых, лунное тяготение далеко не достаёт до Земли. Значит, ни тяготение Солнца, ни тяготение Луны не действуют на вещество Земли, и поэтому традиционный подход совершенно не объясняет истинных причин приливов. В справедливости этого безрадостного для науки вывода легко убедиться. Есть учебники по физике, в которых описывается, каковы приливы должны быть – в согласии с законом всемирного тяготения. А ещё есть учебники по океанографии, в которых описывается, каковы они, приливы, на самом деле. Если традиционный подход был бы верен, и океанская вода притягивалась бы, в том числе, к Солнцу и Луне, то «физическая» и «океанографическая» картины приливов совпадали бы. В действительности же, эти две картины не имеют между собой ничего общего – они кардинально различаются как качественно, так и количественно. Нам ведь ещё в школе вдалбливали, что из-за действия, например, лунного тяготения, в Мировом океане формируется приливный эллипсоид, один горб которого находится на стороне Земли, обращённой к Луне, а другой – на противоположной стороне. И, из-за суточного вращения Земли, эти два горба прокатываются по Мировому океану, отчего в каждом месте получается по два прилива и два отлива за сутки. Однако, перемещение приливного горба означает перетекание колоссальных масс воды из океана в океан – чего в действительности не происходит, ибо каждый океан успешно обходится своими собственными водными ресурсами. Более того, каждый океан разделён на смежные области, в которых приливные явления происходят, практически, автономно. И заключаются они в том, что, в каждой такой области, уровневая поверхность несколько наклонена к горизонту, причём направление этого наклона вращается. Это и есть вращающаяся приливная волна – как в тазике с водой, который двигают по полу круговыми движениями. При этом максимум и минимум уровня последовательно проходят по всему периметру. Ещё Лапласа изумлял этот парадокс: отчего в портах одного и того же побережья полная вода наступает с заметными последовательными запаздываниями – хотя, по концепции приливных эллипсоидов, она должна наступать одновременно. Дело ведь не в том, что «приливным горбам» мешают прокатываться материки. Тихий океан простирается почти на половину окружности экватора, и движения приливных горбов, имей они место, были бы здесь заметны. Но – ничего подобного: и здесь наблюдается устойчивая разбивка на области с независимыми друг от друга вращениями уровневых поверхностей. Никаких намёков на перемещение глобальных волн! Вращение независимых локальных волн – и всё! Океанографы честно изложили это физикам, надеясь получить разумное объяснение. Физики, не напрягаясь, заявили, что вращающиеся волны получаются оттого, что на движущиеся приливные горбы действует сила Кориолиса. Океанографы почесали затылки… как же могуча сила этого Кориолиса! Она так действует на движущиеся приливные горбы, что от них вообще ничего не остаётся – на протяжении всей истории наблюдений за приливами! Поняли океанографы, что с физиками лучше не связываться. Впрочем, физики выжали из феномена вращающихся приливных волн всё, что смогли. Они, зная про этот феномен, умудрялись находить подтверждения даже для ньютоновской статической теории приливов – согласно которой, максимальная амплитуда прилива в новолуние или полнолуние, когда возмущения от Луны и Солнца складываются, должна составлять величину около 90 см. Составили скромный списочек пунктов в центральных областях океанов, где всё примерно так и есть: и на острове Св.Елены – 80 см, и на острове Гуам – столько же, и на островах Антиподов – 1.5 м… Мол, полный триумф ньютоновской теории! – если умолчать о том, что все эти пункты находятся на промежуточных радиусах вращающихся волн. А как же быть с их центральными областями – где высоты приливов, практически, нулевые? А как быть с их периферийными областями – где, на материковых побережьях, высоты приливов, в среднем, составляют чуть поболе двух метров? И эти высоты – без учёта подпора воды в узких бухтах, они характеризуют силу приливообразующего воздействия в чистом виде, как это и обозначено на картах приливов. В общем, практика с полной определённостью показывает: на основе ньютоновской статической теории предвычислять приливы невозможно. Поэтому предвычисления делают с помощью т.н. динамических теорий приливов. Собственно, теориями они называются лишь из вежливости. Ибо, для каждого порта или иного пункта, динамику уровня океана моделируют суммой колебаний с характерными периодами, амплитудами и фазами – которые находят чисто эмпирически. Затем экстраполируют эту сумму колебаний вперёд – вот и получаются предвычисления. А чтобы штурманам не слишком бросалась в глаза неприменимость закона всемирного тяготения к предвычислениям приливов, теоретики придумали изумительную вещь: «отдельные простые колебания рассматриваются… как самостоятельные приливы, обусловленные действием воображаемых фиктивных светил… С этой точки зрения суммарный лунно-солнечный прилив состоит из множества колебаний, вызываемых многими фиктивными светилами» [Д3]. В переводе на общепонятный язык это означает, что, в рамках закона всемирного тяготения, фиктивные светила колеблют океаны в куда лучшем согласии с реальностью, чем их колебали бы Луна и Солнце. Прости этих теоретиков, Ньютон! А в чём же заключаются настоящие причины вращающихся приливных волн? Смотрите: успокоившаяся водная поверхность ортогональна к местной вертикали. Если местная вертикаль совершает вращательные уклонения, то водная поверхность будет отслеживать эти уклонения, стремясь сохранять ортогональность к вертикали – вот вам и вращающаяся приливная волна. Что же касается причин вращательных уклонений у вертикалей, то соответствующие «солнечный» и «лунный» механизмы отличаются друг от друга. Сначала скажем о «солнечном» механизме. Как мы излагали выше (2.8), не вещество Земли порождает земную частотную воронку. Эта воронка создана чисто программными средствами, а Земля просто удерживается в её центре, вблизи положения равновесия. Если бы земная частотная воронка не двигалась с ускорением, то равновесное положение Земли было бы точно в её центре. Но ускорение-то у земной частотной воронки имеется – из-за орбитального движения вокруг Солнца. Поэтому Земля, из-за своих инертных свойств, несколько сдвинута в своей частотной воронке в противоположную от Солнца сторону. Т.е., центр геоида сдвинут относительно центра земного тяготения – а поскольку спутники, летающие вокруг Земли, притягиваются не к центру геоида, а к центру земного тяготения, то геоид должен быть сдвинут относительно клубка орбит спутников. Именно этим сдвигом можно объяснить некоторые эффекты в работе навигационной спутниковой системы GPS, которые до сих пор не нашли объяснения в рамках принятых моделей. Речь идёт, прежде всего, об уверенно обнаруживаемых суточных вариациях при сличениях наземных атомных часов как с отдельными бортовыми часами GPS, так и с системной шкалой времени GPS [В1]. Если эти вариации обусловлены сдвигом геоида относительно орбит GPS, то по величине вариаций можно судить об этом сдвиге. Размах этих вариаций составляет 6-7 наносекунд. С учётом реальной геометрии измерений, оценка для сдвига геоида относительно орбит GPS, в противоположную от Солнца сторону, составляет ~1.6 м [Г13]. Будучи неучтённым, этот сдвиг приводил бы и к другим систематическим эффектам, например, к рассогласованиям результатов сличений шкал времени наземных лабораторий, проводимых на одном и том же временном интервале через разные спутники. Подобный феномен действительно имеет место [В2]. Разновидностью того же феномена можно считать явление, которое происходит при переключениях на новый рабочий спутник или при изменениях состава рабочего созвездия спутников: в потоке данных появляется «ступенька» - это хорошо известно специалистам. Так вот, при наличии названного сдвига геоида относительно центра земного тяготения, везде на поверхности Земли векторы силы тяжести оказываются направлены не к её центру, а к точке, которая находится ближе к Солнцу на 1.6 м. И, сохраняя свои направления к этой точке в условиях суточного вращения Земли, векторы силы тяжести совершают вращательные уклонения около нормали к местному горизонту. Тогда угол максимального уклонения будет равен, очевидно, отношению сдвига 1.6 м к радиусу Земли, т.е. ~2.5?10-7 рад. И, для вращающейся «солнечной» приливной волны с 1000-километровым радиусом, размах положения уровня на периферии составит ~0.5 м – что соответствует действительности. Нам возразят: если верно вышеизложенное, то «солнечное» приливообразующее воздействие должно иметь суточный период – а приливы-то, мол, наблюдаются полусуточные! Отвечаем: давайте, чтобы не трепаться зря, обратимся к опыту. Ведь вопрос о периоде приливных вариаций силы тяжести элементарно решается с помощью гравиметрических измерений. Главная компонента этих вариаций, согласно закону всемирного тяготения, должна иметь полусуточный период. А что мы видим? Да почти ничего. В литературе имеется изобилие теоретических кривых приливных вариаций силы тяжести, но их экспериментальных кривых, практически, нет. А ведь, учитывая фундаментальность вопроса, можно было ожидать, что экспериментальные кривые должны приводиться если уж не в каждом учебнике, то хотя бы в специализированной литературе! Но – ничего подобного! Э-э, тут что-то не так. И мы поняли – что именно. Нам повезло: мы добрались до раритетного издания – трудов известного геодезиста и гравиметриста А.Я.Орлова [О1]. Он ещё в 1909 (!) году исследовал горизонтальные вариации силы тяжести, экспериментируя с маятниками Цельнера. Такой маятник представляет собой стерженёк с грузиком на одном конце, зафиксированный горизонтально с помощью двух вертикальных струнных растяжек, из которых нижняя прикреплена к свободному концу стерженька, а верхняя – к точке, немного отстоящей от свободного конца. Это бесхитростное устройство практически не реагирует на вертикальные возмущения, но обладает исключительно высокой чувствительностью к горизонтальным возмущениям. Труды А.Я.Орлова особенно ценны тем, что в них опубликованы ряды «сырых» данных, а также описаны применявшиеся методики их обработки – любой желающий имеет возможность убедиться в корректности конечных результатов. Приведём один из результатов серии измерений в Юрьеве (Тарту) с тем маятником, который был ориентирован вдоль меридиана. Результаты всей весенне-осенней серии измерений обрабатывались так, чтобы разделить солнечные и лунные эффекты. Рис.2.15 демонстрирует реакцию маятника на солнечные воздействия ([О1], стр.175, таблица 10). Так вот в чём дело! Суточная компонента, оказывается, доминирует – к прискорбию для закона всемирного тяготения! Тогда понятно, почему об этом помалкивают. Мы ещё недоумевали – как это труды Орлова оказались изданы? А дело, по-видимому, в том, что он свои данные представил не в графическом, а в табличном виде – при этом страшная правда о суточных вариациях силы тяжести не слишком бросалась в глаза! Спрашивается: неужели ни у кого, кроме Орлова, не проявлялись суточные вращательные уклонения местных отвесных линий? Ну, что вы – они проявлялись многократно, начиная ещё со второй половины XIX века. Астрономы-то, определяя положения звёзд с помощью своих телескопов, использовали в качестве опорной линии местную вертикаль, реализуемую с помощью ртутного горизонта. Если местные вертикали «гуляют», а в расчёт это не принимается, то, конечно, будут «гулять» положения звёзд: «Основной вывод… заключается в том, что существуют суточные колебания в наблюдённых зенитных расстояниях с амплитудой 0?.16» [К7]. Были специально организованы наблюдения в пунктах с противоположными долготами – и обнаружилось, что сдвиги «наблюдённых зенитных расстояний» звёзд происходят в этих пунктах в противофазе [К7]. Так и должно быть при суточных вращательных уклонениях местных вертикалей.
Рис.2.15 Но признать эти уклонения – значит, вынести приговор закону всемирного тяготения. Поэтому теоретики решили делать вид, что наблюдаемые колыхания звёзд происходят из-за колыханий самой Земли. Мол, противофазные сдвиги «наблюдённых зенитных расстояний» в пунктах с противоположными долготами как раз и означают, что Земля накренилась – отчего широты этих пунктов получили противоположные приращения. Вы, дорогой читатель, небось, думали, что северный и южный полюса Земли находятся на оси её вращения? А вот специалисты по вращению Земли полагают, что её полюса гуляют – из-за того, что Земля накреняется туда-сюда. Правда, объяснить это чудо они до сих пор не могут – как это и бывает, когда пытаешься объяснить то, чего нет в реальности. Но Служба определения параметров вращения Земли вполне процветает. Правда, эта служба оповещает желающих лишь о долгопериодических движениях полюса – годичных и т.н. чандлеровских, со средним периодом 428 дней. А про главные, суточные, движения полюса эта служба помалкивает. Не может Земля покачиваться с периодом в сутки – из-за своих инертных свойств. Поэтому, суточные компоненты в потоках данных прилежно отфильтровывают. Иначе весь этот бред про покачивания Земли сразу рухнет [Г15]. И всё это делают ради того, чтобы скрыть прокол закона всемирного тяготения! Но вернёмся к нашим приливам. Лунное приливообразующее воздействие тоже имеет суточный период – только эти сутки не солнечные, а лунные (они длятся примерно 24 час 50 мин). И причина лунных приливов связана с тем самым переменным ускорением Земли «вперёд-назад», вызываемым периодическими ускорениями-замедлениями орбитального движения земной частотной воронки (2.14). Амплитуда вектора этого ускорения, достигаемая в квадратурах, составляет 2.8?10-5 м/с2. Этот вектор входит, как дополнительное слагаемое, в местные вектора силы тяжести на поверхности Земли. Результирующие векторы силы тяжести в каждом пункте, из-за суточного вращения Земли, совершают, опять же, вращательные уклонения – благодаря чему и генерируются вращающиеся приливные волны. Но как получается, что эти волны вращаются с периодом в лунные сутки, а не в солнечные? Дело в том, что вблизи новолуний-полнолуний, при переходе Земли через нулевое колебательное смещение, вектор колебательного ускорения также переходит через ноль и изменяет своё направление в пространстве на противоположное. При этом фазы вращательных уклонений местных вертикалей испытывают скачок на 180о. После этого скачка приливная волна восстанавливает синхронизм со своим генератором – что, из-за инертных свойств воды, занимает некоторое время и осуществляется через небольшое увеличение периода вращения волны. В идеале, если восстановление синхронизма длится половину синодического месяца, то период вращения равен средним лунным суткам. Но обычно максимальные и минимальные размахи суточных приливов запаздывают – иногда на несколько суток – относительно соответствующих фаз колебательного цикла Земли.. Если отбросить поправки на эти запаздывания, то на типичных кривых суточных приливов хорошо видно, что их минимальные, практически, нулевые размахи, приходятся на новолуния-полнолуния, а максимальные – на серединки между ними. Это соответствует изменениям колебательного ускорения Земли и, опять же, противоречит закону всемирного тяготения – согласно которому, высоты приливов должны быть максимальны в полнолуния-новолуния! Добавим, что предсказание закона всемирного тяготения о том, что приливы с полусуточным периодом должны доминировать, также не подтверждается практикой. Из вышеизложенного ясно, что приливообразующих воздействий с полусуточным периодом не существует. И, действительно, в открытых океанах, т.е. на подавляюще большей площади Мирового океана, почти безраздельно властвуют суточные приливы. На окраинных морях наблюдаются смешанные суточно-полусуточные приливы, а в малых морях, проливах и больших бухтах – полусуточные. Традиционно, господство суточного типа приливов в открытых океанах объясняют «большими суточными неравенствами» - как будто склонение Луны проявляется в открытом океане как-то иначе, чем вблизи побережий на тех же широтах. Давайте же обратим внимание на то, что чем меньше площадь и глубина участка океана, в котором вращается приливная волна, тем более смещён в короткопериодическую сторону спектр приливных колебаний этого участка. Напрашивается очевидный вывод: в приливных колебаниях не последнюю роль играют резонансные явления. Эта идея не нова; она высказывалась, например, в [Д3,Ш2], но не получила развития. А ведь наличие резонансов кардинально изменяет физику приливных явлений, поскольку здесь уже не работает принцип линейной суперпозиции возмущающих воздействий. Действительно, здесь отклики на воздействия с различными периодами должны иметь различные «коэффициенты передачи»: сильнее должен быть отклик на то воздействие, период которого ближе к резонансному. Более того, само происхождение полусуточных приливов оказывается следствием генерации второй гармоники при суточном воздействии! В пользу этого вывода свидетельствует и тот факт, что в некоторых малых мелководных областях – например, в Кандалакшском заливе Белого моря – наблюдаются четвертьсуточные приливы [Ш2]! Следствием такого подхода, проверенным нами с помощью несложных машинных экспериментов [Г13], является то, что почти все основные и промежуточные типы приливов оказывается возможным промоделировать, считая их результатами совместного действия всего двух первичных возмущений: солнечно-суточного и лунно-суточного – с допущением генерации вторых гармоник! Итак, учёт феномена вращательных уклонений местных вертикалей ставит на свои места и полюса Земли, и настоящие источники приливных явлений в океанах. А ещё он помогает поставить на место фирму PASCO (2.2), которая производит игрушечные установки для повторения опыта Кавендиша. Правда, разработчики этих игрушек применили важное новшество: подвес коромысла сделан не нитевидным, а ленточным – из бериллиевой меди, с поперечным сечением 0.017х0.150 мм [П5]. В отличие от нитевидного, ленточный подвес и вынуждает коромысло немного довернуться при достаточном для этого уклонении местной вертикали. Причём, доворот произойдёт в том же направлении, что и вращательное уклонение вертикали, т.е. по часовой стрелке, если смотреть сверху. Вот почему изготовители просят [П5], при смене позиций «притягивающих» шаров, не путать, какая позиция является первой, а какая второй – иначе вместо «притяжения» обнаружится «отталкивание». Ну, и ещё: размахи вращательных уклонений местных вертикалей зависят от фаз Луны: они максимальны в квадратурах, а в сизигиях они нулевые. Те, кто уже приобрели установку фирмы PASCO, могут убедиться: в новолуния и полнолуния фирменные болваночки теряют «притягивающие» свойства! Но не всегда гуляния вертикалей являются таким полезным эффектом: толпы геодезистов и гравиметристов уже покрыли их матом во множество слоёв. «Ничего не поделаешь, - разъясняют теоретики, - дело в несовершенстве приборов, у которых имеется дрейф нуля». Да нет, приборы здесь не виноваты: «дрейф нуля сейсмометра, установленного в Ленинграде, подобен дрейфу нуля гравиметра, установленного под Алма-Атой… Такое подобие показаний приборов разной конструкции не может быть объяснено ни аппаратурной погрешностью, ни локальными процессами… временной ход этой глобальной вариации коррелирует с лунными фазами» [А7]. Так что на зеркало неча пенять, коли рожа крива! Ссылки к Разделу 2. А1. К.У.Аллен. Астрофизические величины. «Мир», М., 1977. А2. J.D.Anderson, P.A.Laing, E.L.Lau, et al. Phys.Rev.Lett., 81, 14 (1998) 2858. А3. M.E.Ash, I.I.Shapiro, W.B.Smith. Astr. Journal, 72, 3 (1967) 338. А4. Э.Л.Аким и др. ДАН СССР, т.201, 6 (1971) 1303. А5. J.D.Anderson et al. Science, 167, 3916 (1970) 277. А6. К.Б.Алексеев, Г.Г.Бебенин, В.А.Ярошевский. Маневрирование космических аппаратов. «Машиностроение», М., 1970. А7. Ю.Н.Авсюк, С.Н.Щеглов. ДАН, 288, 1 (1986) 71. Б1. И.И.Блехман, Г.Ю.Джанелидзе. Вибрационное перемещение. «Наука», М., 1964. Б2. B.C.Blevis. Nature, 180, 4577 (1957) 139. В1. M.Weiss. IEEE Trans. Instrum. Meas., 38, 5 (1989) 991. В2. M.A.Weiss, D.W.Allan. IEEE Trans. Instrum. Meas., 36, 2 (1987) 572. ВЕБ1. http://www2.jpl.nasa.gov/galileo/mess35/DACTYL.html ВЕБ2. http://cfa-www.harvard.edu/iauc/07700/07703.html ВЕБ3. http://cfa-www.harvard.edu/iauc/07100/07129.html ВЕБ4. http://cfa-www.harvard.edu/iauc/07500/07503.html ВЕБ5. http://cfa-www.harvard.edu/iauc/08100/08182.html ВЕБ6. http://cfa-www.harvard.edu/iauc/08900/08980.html ВЕБ7. http://www.astronet.ru/db/msg/1189784/index.html ВЕБ8. http://www.johnstonsarchive.net/astro/asteroidmoons.html ВЕБ9. http://www.novosti-kosmonavtiki.ru/content/numbers/216/29.shtml ВЕБ10. http://www.ntsomz.ru/news/news_cosmos/haiabusa_16_september_2005 ВЕБ11. http://www.cnews.ru/news/top/index.shtml?2005/11/15/191506 ВЕБ12. http://cfa-www.harvard.edu/iau/lists/InnerPlot.html ВЕБ13. http://galspace.spb.ru/index71.html ВЕБ14. http://astrologic.ru/kbo/pojas_k.htm ВЕБ15. http://kabmir.com/nauka/13_faktov_ne_imejushhih_nauchnogo_objasnenija.html ВЕБ16. http://nssdcftp.gsfc.nasa.gov/spacecraft_data/ ВЕБ17. www.novosti-kosmonavtiki.ru/content/numbers/193/37.shtml ВЕБ18. www.astronaut.ru/luna/usa_a.htm ВЕБ19. www.universetoday.com/2007/11/05/change-1-enters-lunar-orbit/ ВЕБ20. www.jaxa.jp/press/2007/10/20071005_kaguya_e.htm ВЕБ21. www.astronaut.ru/luna/japan_a.htm ВЕБ22. http://www.novosti-kosmonavtiki.ru/phpBB2/viewtopic.php?t=1111 ВЕБ23. http://offizika.narod.ru , темка «Трагикомедия с зондом SMART-1». ВЕБ24. http://sci.esa.int/science-e/www/object/index.cfm?fobjectid=39719 ВЕБ25. http://www.astrolab.ru/cgi-bin/print.cgi?s=manager&id=33num=495 ВЕБ26. http://vo.obspm.fr/exoplanetes/encyclo/biblio.php ВЕБ27. www.allplanets.ru/history.html ВЕБ28. http://neic.usgs.gov ВЕБ29. http://offizika.narod.ru , темка «Аномальное ускорение «Пионеров». ВЕБ30. http://www.cnews.ru/news/top/index.shtml?2005/11/21/191881 Г1. «Г.Кавендиш. Определение плотности Земли». В: Г.М.Голин, С.Р.Филонович. Классики физической науки. «Вышайшая школа», Минск, 1989. Стр. 253-268. Г2. J.H.Gundlach, S.M.Merkowitz. Phys.Rev.Lett., 85, 14 (2000) 2869. Г3. А.А.Гришаев. Форма геоида и опыт Кавендиша: как совместить несовместимое. – Доступна на сайте http://newfiz.narod.ru Г4. А.А.Гришаев. Взаимное тяготение звёзд и планет обусловлено… алгоритмически? – Там же. Г5. А.А.Гришаев. О всемирном тяготении: всё ли вещество оказывает притягивающее действие? – Там же. Г6. А.А.Гришаев. Вертикальное свободное падение: новые нижние ограничения на скорость действия тяготения. – Там же. Г7. А.А.Гришаев. Энергетика свободного падения. – Там же. Г8. А.А.Гришаев. Феномен астероидов-Троянцев и модель «унитарного» действия тяготения. – Там же. Г9. А.А.Гришаев. Внешний край пояса Койпера – граница области солнечного тяготения. – Там же. Г10. А.А.Гришаев. Граница области тяготения Луны: анализ полётов в окололунном пространстве. – Там же. Г11. А.А.Гришаев. Свидетельства об одномерности колебаний Земли в кинематике пары Земля-Луна. – Там же. Г12. А.А.Гришаев. Синхронизатор орбитального движения Луны. – Там же. Г13. А.А.Гришаев. Новый взгляд на природу приливообразующих сил. – Там же. Г14. А.А.Гришаев. «Зыбкое пространство», порождающее собственное тяготение Луны. – Там же. Г15. А.А.Гришаев. Периодическое движение полюсов Земли: реальность или иллюзия? – Там же. Г16. А.А.Гришаев. Организация тяготения в «цифровом» физическом мире. Серия «Проблемы исследования Вселенной», вып.34. Труды Конгресса-2010 «Фундаментальные проблемы естествознания и техники», Часть I, стр.165. С-Пб., 2010. Г17. А.А.Гришаев. Имеют ли собственное тяготение малые тела Солнечной системы? – Доступна на сайте http://newfiz.narod.ru Д1. Планеты и спутники. Под ред. А.Дольфюса. Пер. с англ. и фр. под ред. В.Г.Курта. «Мир», М., 1974. Д2. Справочное руководство по небесной механике и астродинамике. Г.Н.Дубошин, ред. «Наука», М., 1976. Д3. А.И.Дуванин. Приливы в море. «Гидрометеорологическое изд-во», Л., 1960. З1. А.Зеберг, частное сообщение. К1. T.J.Quinn, et al. Phys.Rev.Lett., 87, 11 (2001) 111101-1. К2. Таблицы физических величин. Справочник под ред. акад. И.К. Кикоина. «Атомиздат», М., 1976. К3. E.B.Fomalont, S.M.Kopeikin. The measurement of the light deflection from Jupiter: experimental results. Astrophys. Journal, 598 (2003) 704-711. Электронная версия: http://xray.sai.msu.ru/?polar/sci_rev/03_02_17-21.html#astro-ph/0302294 К4. С.М. Копейкин, Э.Фомалонт. Фундаментальный предел скорости гравитации и его измерение. Земля и Вселенная, №3/2004. Электронная версия: http://ziv.telescopes.ru/rubric/hypothesis/?pub=1 К5. Космонавтика. Энциклопедия. В.П.Глушко, гл. ред. «Сов. энциклопедия», М., 1985. К6. Физика и астрономия Луны. З.Копал, ред. «Мир», М., 1973. К7. К.А.Куликов. Изменяемость широт и долгот. «Гос. изд-во физико-математической литературы», М., 1962. Л1. G.G.Luther, W.A.Towler. Phys.Rev.Lett., 48, 3 (1982) 121. Л2. Пьер Симон Лаплас. Изложение системы мира. «Наука», Л., 1982. Л3. Л.Д.Ландау, Е.М.Лифшиц. Теория поля. «Наука», М., 1967. Л4. В.И.Левантовский. Механика космического полёта в элементарном изложении. «Наука». М., 1974. Л5. В.И.Левантовский. Ракетой к Луне. «Гос. изд-во физико-математической литературы», М., 1960. Л6. G.Latham et al. Science, 170, 3958 (1970) 620. М1. В.А. Магницкий. Основы физики Земли. «Геодезиздат», М., 1953. М2. Планеты и спутники. Пер. с англ. под ред. В.И.Мороза. «Изд-во иностранной литературы», М., 1963. М3. Р.Манчестер, Дж.Тейлор. Пульсары. «Мир», М., 1980. М4. D.O.Muhleman et al. Astr. Journal, 67, 4 (1962) 191. Н1. А.Николаевский. «Тропа иссушающая». Веб-ресурс http://andmbe.euro.ru О1. А.Я.Орлов. Избранные труды, т.2. «Изд-во АН УССР», Киев, 1961. П1. В.В.Прокофьева, В.П.Таращук, Н.Н.Горькавый. УФН, 165, 6 (1995) 661. П2. R.V.Pound, G.A.Rebka. Phys.Rev.Lett., 4 (1960) 337. П3. G.H.Pettingill et al. Astr. Journal, 72, 3 (1967) 330. П4. www.pasco.com П5. ftp://ftp.pasco.com/Support/Documents/English/AP/AP-8215A/012-11032A.pdf Р1. R.D.Rose et al. Phys.Rev.Lett., 23, 12 (1969) 655. С1. М.У.Сагитов. Постоянная тяготения и масса Земли. «Наука», М., 1969. С2. М.У.Сагитов и др. ДАН СССР, 245, 3 (1979) 567. С3. О.Струве, Б.Линдс, Э.Пилланс. Элементарная астрономия. «Наука», М., 1967. С4. М.Ф.Субботин. Введение в теоретическую астрономию. «Наука». М., 1968. С5. Ф.Г.Смит. Пульсары. «Мир», М., 1979. С6. F.D.Stacey, et al. Phys.Rev.D, 23, 8 (1981) 1683. У1. Участники телеконференций в Интернете, частные сообщения. Ф1. T. Van Flandern. The speed of gravity – what the experiments say. Phys.Lett. A, 250 (1998) 1. Ц1. Т. Цубои. Гравитационное поле Земли. М., Мир, 1982. Ч1. Б.Е.Черток. Ракеты и люди. Кн.2: Фили-Подлипки-Тюратам. «Машинострение», М., 1999. Стр.252. Ш1. Б.П. Шимбирев. Теория фигуры Земли. М., Недра, 1975. Ш2. В.В.Шулейкин. Очерки по физике моря. «Изд-во АН СССР». М.-Л., 1949. |
|
|||
|
Главная | Контакты | Прислать материал | Добавить в избранное | Сообщить об ошибке |
||||
|
|
||||

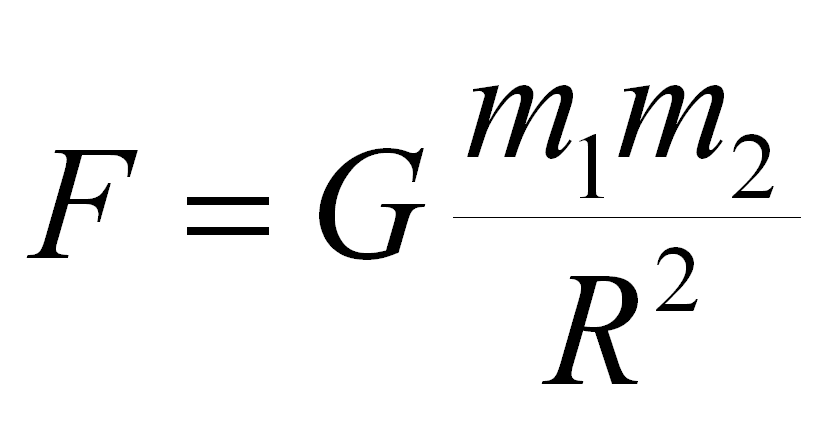 , (2.1.1)
, (2.1.1)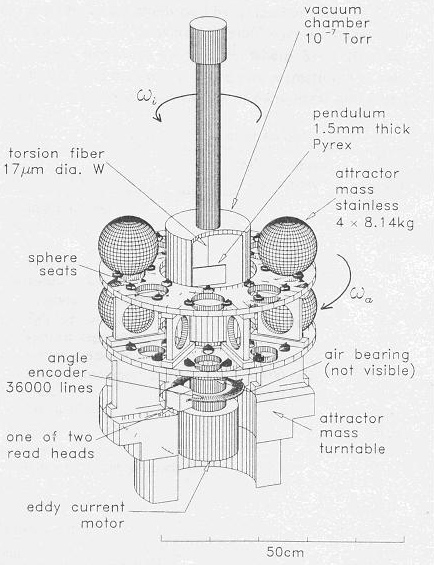
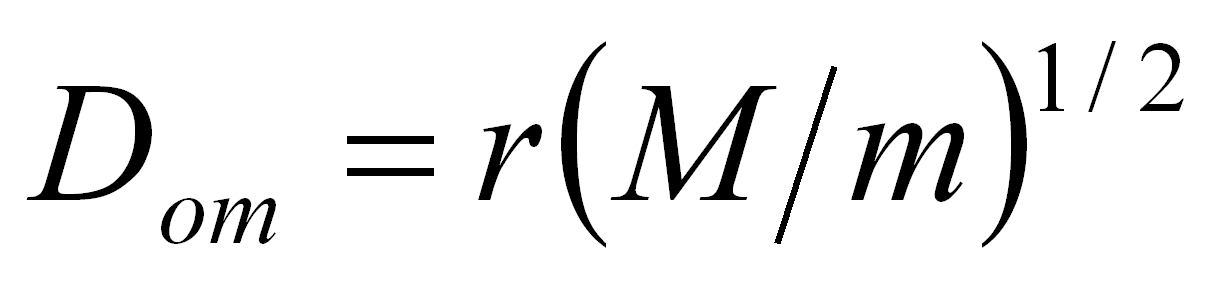 .
.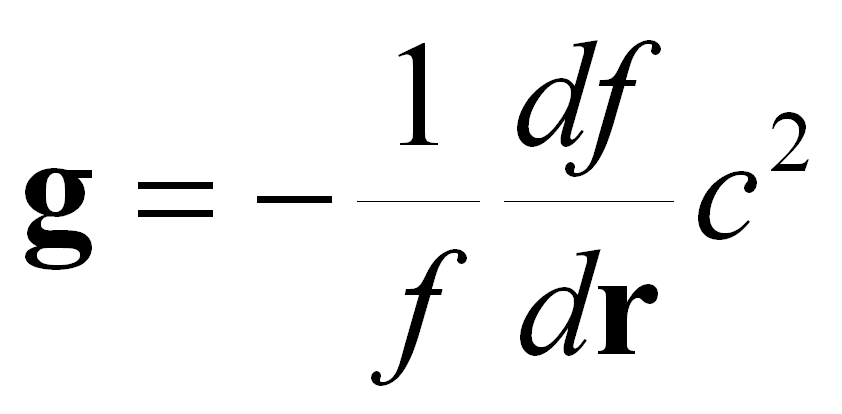 , (2.7.1)
, (2.7.1)