Для определения прямой необходимы две точки. Точку определяют две проекции на горизонтальную и фронтальную плоскости, т. е. прямая определяется с помощью проекций двух своих точек на горизонтальной и фронтальной плоскостях.

На рисунке 17 показаны проекции (а и a?, b и b?) двух точек А и В. С их помощью определяется положение некоторой прямой АВ. При соединении одноименных проекций этих точек (т. е. а и b, а? и b?) можно получить проекции аb и а?b? прямой АВ.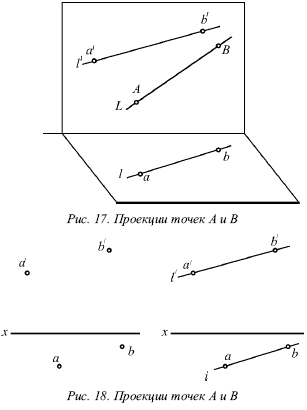

На рисунке 18 показаны проекции обеих точек, а на рисунке 19 – проекции проходящей через них прямой линии.

Если проекции прямой определяются проекциями двух ее точек, то они обозначаются двумя рядом поставленными латинскими буквами, соответствующими обозначениям проекций точек, взятых на прямой: со штрихами для обозначения фронтальной проекции прямой или без штрихов – для горизонтальной проекции.

Если рассматривать не отдельные точки прямой, а ее проекции в целом, то данные проекции обозначаются цифрами.

Если некоторая точка С лежит на прямой АВ, ее проекции с и с? находятся на одноименных проекциях прямой ab и а?b?. Данную ситуацию поясняет рисунок 19.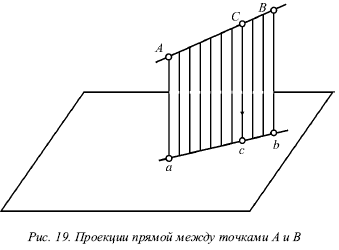

След прямой – это точка пересечения ее с некоторой плоскостью или поверхностью (рис. 20).

Горизонтальным следом прямой называется некоторая точка H, в которой прямая встречается с горизонтальной плоскостью, а фронтальным – точка V, в которой данная прямая встречается с фронтальной плоскостью (рис. 20).

На рисунке 21а изображен горизонтальный след прямой, а ее фронтальный след, – на рисунке 21б.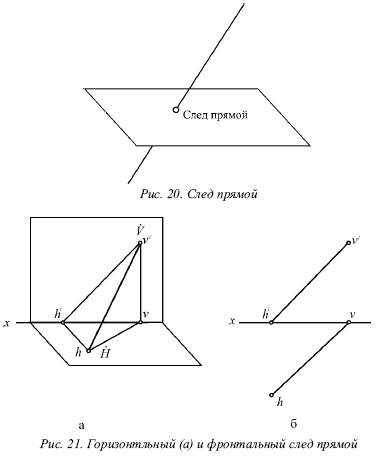

Иногда также рассматривается профильный след прямой, W – точка пересечения прямой с профильной плоскостью.

Горизонтальный след находится в горизонтальной плоскости, т. е. его горизонтальная проекция h совпадает с этим следом, а фронтальная h? лежит на оси х. Фронтальный след лежит во фронтальной плоскости, поэтому его фронтальная проекция ?? совпадает с ним же, а горизонтальная v лежит на оси х.

Итак, H = h, и V = ??. Следовательно, для обозначения следов прямой можно применять буквы h и ??.

Прямую называют прямой общего положения, если она не параллельна и не перпендикулярна ни одной плоскости проекций. Проекции прямой общего положения тоже не параллельны и не перпендикулярны осям проекций.

Прямые, которые параллельны одной из плоскостей проекций (перпендикулярны одной из осей). На рисунке 22 показана прямая, которая параллельна горизонтальной плоскости (перпендикулярная оси z), – горизонтальная прямая; на рисунке 23 показана прямая, которая параллельна фронтальной плоскости (перпендикулярна оси у), – фронтальная прямая; на рисунке 24 показана прямая, которая параллельна профильной плоскости (перпендикулярна оси х), – профильная прямая. Несмотря на то что каждая из данных прямых образует с одной из осей прямой угол, они не пересекают ее, а только скрещиваются с нею.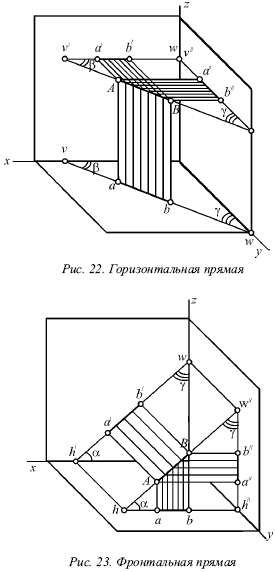

Из-за того что горизонтальная прямая (рис. 22) параллельна горизонтальной плоскости, ее фронтальная и профильная проекции будут параллельны осям, определяющим горизонтальную плоскость, т. е. осям х и у. Поэтому проекции a?b?|| х и a?b?|| у, т. е. они перпендикулярны оси z. Горизонтальная проекция ab может занимать любое положение на эпюре.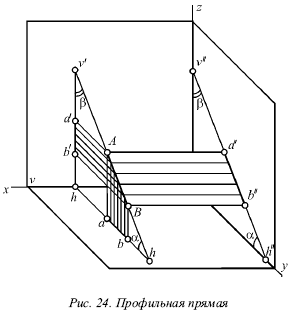

У фронтальной прямой (рис. 23) проекции аb || x и a?b? || z, т. е. они перпендикулярны оси у, а потому в этом случае фронтальная проекция а?b? прямой может занимать произвольное положение.

У профильной прямой (рис. 24) аb || у, а?b|| z, и обе они перпендикулярны оси х. Проекция а?b? может располагаться на эпюре любым образом.

При рассмотрении той плоскости, которая проецирует горизонтальную прямую на фронтальную плоскость (рис. 22), можно заметить, что она проецирует эту прямую и на профильную плоскость, т. е. она является плоскостью, которая проецирует прямую сразу на две плоскости проекций – фронтальную и профильную. Исходя из этого ее называют дважды проецирующей плоскостью. Таким же образом для фронтальной прямой (рис. 23) дважды проецирующая плоскость проецирует ее на плоскости горизонтальной и профильной проекций, а для профильной (рис. 23) – на плоскости горизонтальной и фронтальной проекций.

Две проекции не могут определить прямую. Две проекции 1 и 1? профильной прямой (рис. 25) без уточнения на них проекций двух точек этой прямой не определят положения данной прямой в пространстве.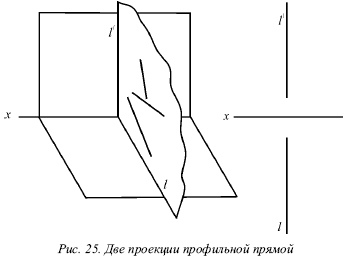

В плоскости, которая перпендикулярна двум заданным плоскостям симметрии, возможно существование бесчисленного множество прямых, для которых данные на эпюре 1 и 1? являются их проекциями.

Если точка находится на прямой, то ее проекции во всех случаях лежат на одноименных проекциях этой прямой. Обратное положение не всегда справедливо для профильной прямой. На ее проекциях можно произвольным образом указать проекции определенной точки и не быть уверенным в том, что эта точка лежит на данной прямой.

Во всех трех частных случаях (рис. 22, 23 и 24) положения прямой по отношению к плоскости проекций произвольный ее отрезок АВ, взятый на каждой из прямых, проецируется на одну из плоскостей проекций без искажения, т. е. на ту плоскость, которой он параллелен. Отрезок АВ горизонтальной прямой (рис. 22) дает проекцию в натуральную величину на горизонтальную плоскость (аb = АВ); отрезок АВ фронтальной прямой (рис. 23) – в натуральную величину на плоскость фронтальной плоскости V (a?b? = AB) и отрезок АВ профильной прямой (рис. 24) – в натуральную величину на профильную плоскость W (a?b? = АВ), т. е. представляется возможным измерить на чертеже натуральную величину отрезка.

Иначе говоря, с помощью эпюр можно определить натуральные размеры углов, которые рассматриваемая прямая образует с плоскостями проекций.

Угол, который составляет прямая с горизонтальной плос костью Н, принято обозначать буквой ?, с фронтальной плоскостью – буквой ?, с профильной плоскостью – буквой ?.

Любая из рассматриваемых прямых не имеет следа на параллельной ей плоскости, т. е. горизонтальная прямая не имеет горизонтального следа (рис. 22), фронтальная прямая не имеет фронтального следа (рис. 23), а профильная прямая – профильного следа (рис. 24).

Возможны три случая расположения прямых в пространстве:

1) прямые пресекаются, т. е. имеют общую точку;

2) прямые параллельны, т. е. не имеют общей точки, но лежат в одной плоскости;

3) прямые скрещиваются, т. е. не лежат в одной плоскости, т. е. через них нельзя провести плоскость.

Когда прямые пересекаются, на эпюре точки пересечения их одноименных проекций на горизонтальной и фронтальной плоскостях находятся на одном перпендикуляре к оси х.

Рассмотрим прямые I и II, которые пересекаются в точке А (рис. 26). Спроецируем обе прямые на горизонтальную плоскость. Если учесть, что точка А принадлежит обеим прямым, то ее проекция а будет принадлежать также и обеим проекциям прямых.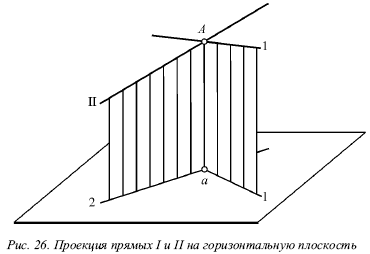

Похожая картина будет и на фронтальной плоскости, т. е. эти точки пересечения одноименных проекций а и а? являются проекциями некоторой точки А, и поэтому они должны лежать на одном перпендикуляре к оси х. Точно так же будет верным и обратное утверждение: если на эпюре точки пересечения одноименных проекций прямых на две плоскости (горизонтальную и фронтальную) лежат на одном перпендикуляре к оси х, то эти прямые пересекаются.

Пусть проекции прямых I к II (рис. 27) подчиняются этому условию.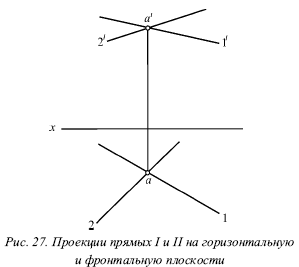

Тогда точки пересечения их одноименных проекций можно рассматривають как проекции некоторой точки в пространстве. Обозначим точку пересечения горизонтальных проекций 1 и 2 буквой а, а точку пересечения фронтальных проекций 1? и 2? – буквой а?. Рассматриваемая точка А находится и на прямой I, и на прямой II. То есть она является их общей точкой, в которой пересекаются эти прямые.

Прямое утверждение справедливо во всех случаях без исключения. Обратное же утверждение неприменимо в том случае, если хотя бы одна из прямых профильная.

Когда прямые параллельны, на эпюре их одноименные проекции параллельны (рис. 28).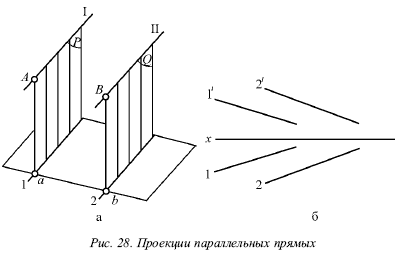

На самом деле, плоскости Р и Q, проецирующие прямые I и II на горизонтальную плоскость, параллельны, так как в каждой из этих плоскостей можно указать две пересекающиеся прямые, параллельные двум пересекающимся прямым второй плоскости, т. е. прямая I параллельна прямой II, и проектирующий луч Аа параллелен лучу Вb. Но две параллельные плоскости Р и Q пересекут горизонтальную плоскость. В результате этого образуются две параллельные прямые 1 и 2, т. е. горизонтальные проекции прямых I и II параллельны между собой.

Аналогично можно доказать, что и любые другие одноименные проекции обеих прямых также будут параллельны друг другу.

Верно и обратное утверждение: прямые параллельны, если на эпюре их одноименные проекции параллельны.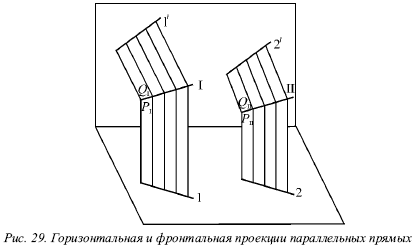

Если известно, что горизонтальные и фронтальные проекции прямых I и II параллельны, будет справедливо следующее: 1 || 2 и 1?|| 2? (рис. 29).

В этом случае можно сказать, что плоскости Р_I и Р_II, проецирующие прямые I и II на горизонтальную плоскость, параллельны, так как в этих плоскостях можно указать по паре пересекающихся соответственно параллельных прямых (прямые 1 и 2 и проецирующие лучи). Аналогично плоскости Q_I и Q_II будут параллельны.

Прямая I находится в пересечении плоскостей Р_I и Q_I, а прямая II – в пересечении плоскостей Р_II Q_II. Отсюда получаем, что прямая I параллельна плоскости Р_II, потому что находится в плоскости, ей параллельной. Однако прямая I параллельна и плоскости Q_II. Поэтому прямая I параллельна линии пересечения плоскостей Р_II и Q_II, т. е. прямой II.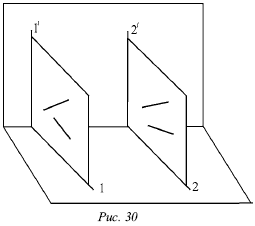

Доказательство обратного утверждения не имеет смысла для профильных прямых. Это объясняется тем, что тогда вместо двух плоскостей, проецирующих прямую на горизонтальную и фронтальную плоскости, существует только одна, дважды проецирующая плоскость (рис. 30).

Видно, что вне зависимости от расположения двух профильных прямых I и II в пространстве их горизонтальные и фронтальные проекции всегда параллельны (или сливаются).

Прямые будут являться скрещивающимися, если они не параллельны и не пересекаются. Это вытекает из того, что возможны только три случая взаимного расположения прямых.

Для скрещивающихся прямых справедливы утверждения:

1) точки пересечения одноименных проекций на горизонтальной и фронтальной плоскостях не лежат на одном перпендикуляре к оси х (прямые I и II на рис. 31).

2) хотя бы в одной паре одноименные проекции не параллельны (прямые III и IV на рис. 31).

Рисунок 31 показывает проекции четырех прямых, любая пара из которых скрещивается.

Как и в рассмотренных ранее случаях, обратное утверждение для скрещивающихся прямых несправедливо при условии, что хотя бы одна из прямых является профильной.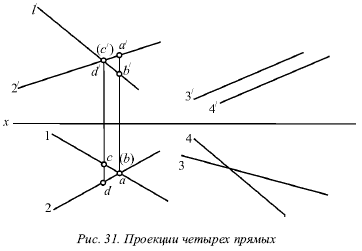

Рассмотрим теорему: если одна сторона прямого угла параллельна плоскости проекций (или лежит в ней), то прямой угол проецируется на эту плоскость без искажения.

Приведем доказательство для прямого угла ABC, одна сторона которого ВС параллельна горизонтальной плоскости (рис. 32).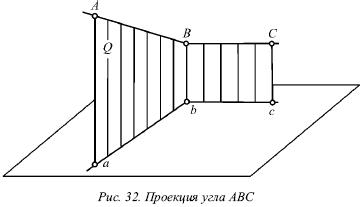

Плоскость, в которой находится сторона угла АВ и ее проекция ab, перпендикулярна горизонтальной плоскости, так как содержит перпендикуляр Вb к этой плоскости. Прямая ВС перпендикулярна плоскости Q вследствие ее перпендикулярности двум пересекающимся прямым этой плоскости (АВ и Вb). Прямая bc параллельна ВС, т. е. она также перпендикулярна Q, а значит и прямой ab, которая лежит в ней.

Ясно, что если на эпюре одна пара одноименных проекций двух прямых перпендикулярна, а одна из двух остальных проекций параллельна оси х, то такие прямые образуют в пространстве прямой угол.

Предположим, что ab ?bc, b?с? || x.

Это показано на рисунке 33.

Можно провести через проекцию аb плоскость Q, проектирующую прямую АВ на горизонтальную плоскость (рис. 33). Проекция bс перпендикулярна плоскости Q вследствие того, что она перпендикулярна двум прямым этой плоскости, т. е. проекции аb (по условию), и проецирующему лучу Вb как перпендикуляру горизонтальной плоскости.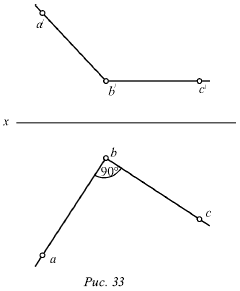

Прямая ВС является параллельной горизонтальной плоскости, так как ее фронтальная проекция bс параллельна оси х, поэтому она параллельна своей горизонтальной проекции, т. е. справедливо выражение ВС || bс. Следовательно, прямая ВС перпендикулярна плоскости Q и поэтому перпендикулярна прямой АВ вне зависимости от ее положения в плоскости Q.

Через некоторую точку М можно провести огромное количество прямых, которые перпендикулярны данной прямой АВ. Они образуют целую плоскость Р, перпендикулярную АВ (рис. 34).

Из всех перпендикулярных прямых, которые при этом образуются, только одна пересекает данную прямую. Это прямая MN, которая проходит через точку N пересечения прямой АВ и плоскости Р.

Под перпендикуляром к прямой подразумевается прямая, не только перпендикулярная данной прямой, но и пересекающая в отличие от просто перпендикулярных скрещивающиеся прямые.

Прямой угол между скрещивающимися прямыми проецируется на данную плоскость проекций без искажения, если одна из прямых параллельна этой плоскости или лежит в ней.